
Intersección de conjuntos
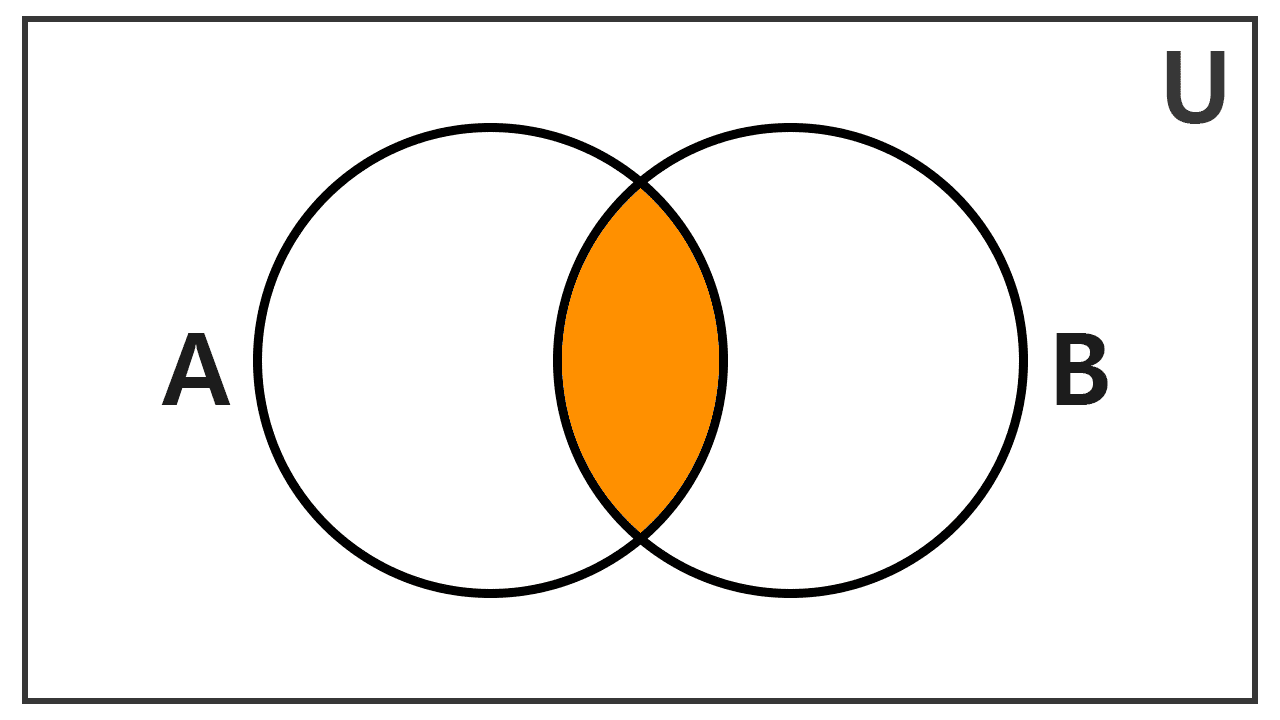
La intersección de conjuntos es una operación fundamental que produce un nuevo conjunto formado únicamente por los elementos que comparten los conjuntos originales, es decir, los elementos repetidos. Se representa mediante el símbolo “∩”.
Formalmente, la intersección de dos conjuntos A y B se define como el conjunto de todos los elementos que pertenecen tanto a A como a B. Se denota como A ∩ B y se expresa por comprensión de la siguiente manera:
A ∩ B = { x | x ∈ A ∧ x ∈ B }
En esta definición se utiliza una conjunción (el conectivo lógico "y"), lo que significa que un elemento solo formará parte de la intersección si está presente en ambos conjuntos a la vez.
La diferencia principal entre la unión y la intersección radica en los elementos que incluyen: mientras la unión agrupa todos los elementos de los conjuntos involucrados, la intersección se limita exclusivamente a aquellos que son comunes a todos ellos.
Índice
Ejemplos
A continuación, veremos varios casos de intersección de conjuntos. Es clave saber que, si no hay elementos comunes, el resultado será el conjunto vacío (Ø), y los conjuntos cuya intersección es vacía se llaman disjuntos.
Ejemplo 1
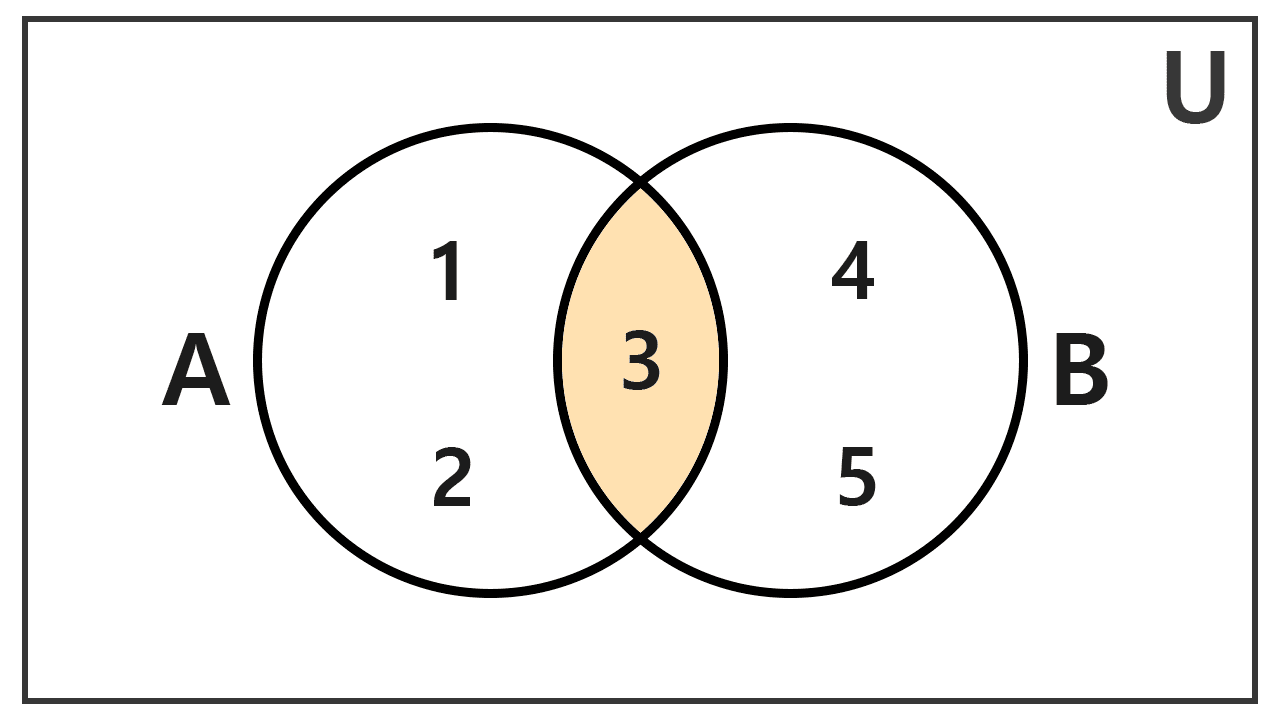
Sean los conjuntos A = {1, 2, 3} y B = {3, 4, 5}. Hallar su intersección.
Solución
Identificamos los elementos que están presentes en ambos conjuntos. Observamos que solo el número 3 cumple esta condición. Por lo tanto, la intersección es:
A ∩ B = {3}
Gráficamente la solución es:
Ejemplo 2
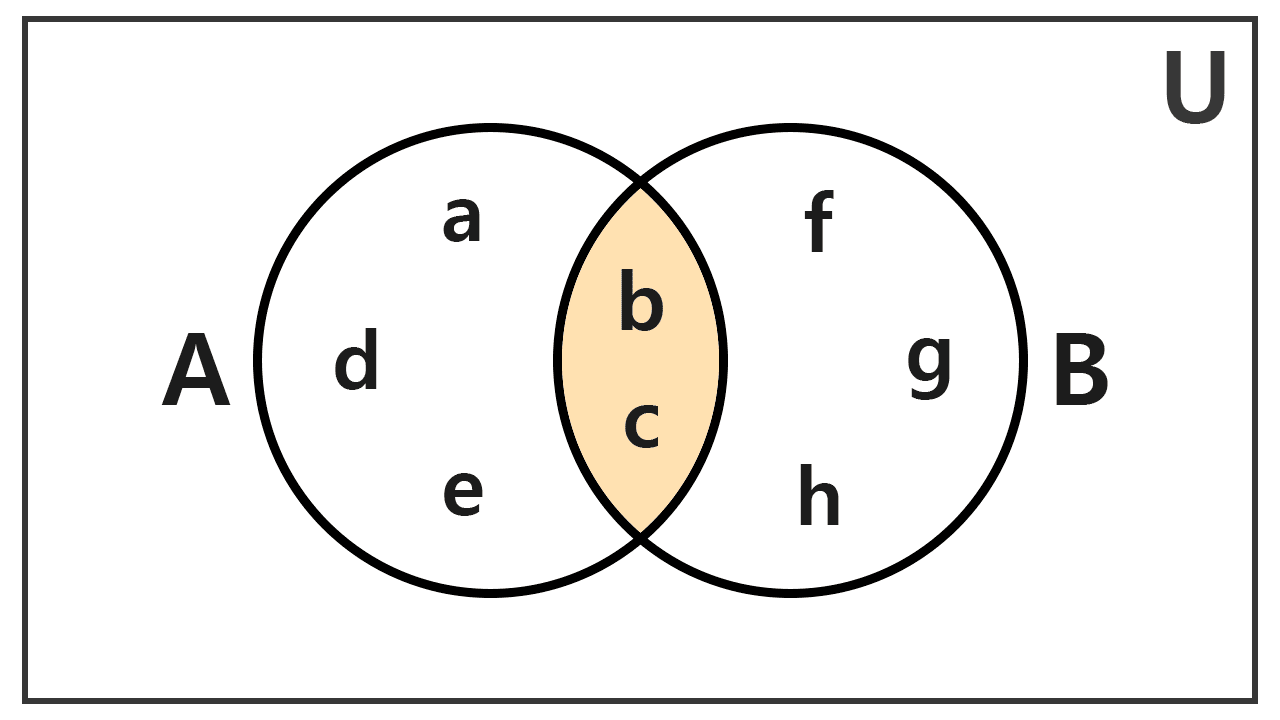
Determinar la intersección de A = {a, b, c, d, e} y B = {b, c, f, g, h}.
Solución
Buscamos los elementos que pertenecen a A y a B de manera simultánea. Las letras 'b' y 'c' son las únicas que aparecen en ambos. Así, el conjunto intersección queda:
A ∩ B = {b, c}
Ejemplo 3
Calcular la intersección de E = {-1, -2, -3} y F = {1, 2, 3}.
Solución
En este caso, los conjuntos E y F no tienen ningún elemento en común, son conjuntos disjuntos. La intersección de dos conjuntos disjuntos es siempre el conjunto vacío:
E ∩ F = ∅
Ejemplo 4
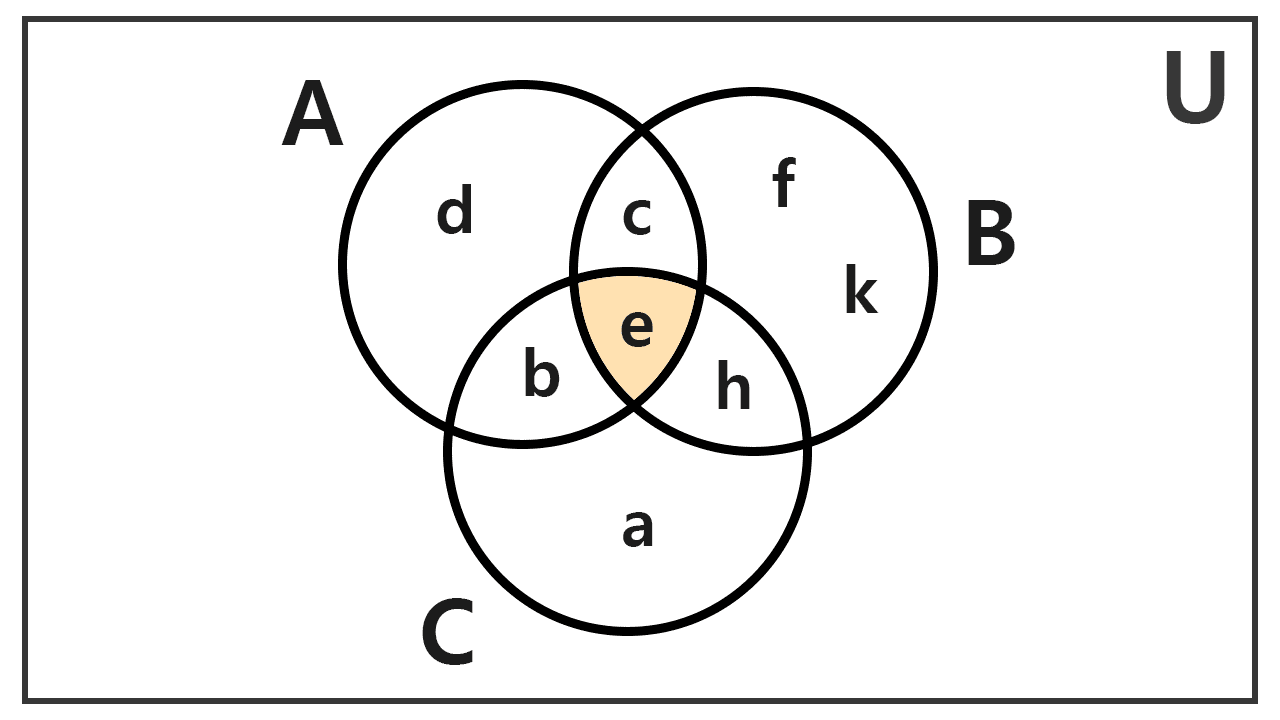
Dados los conjuntos A = {b, c, d, e}, B = {c, e, h, f, k} y C = {a, b, e, h}, calcular la intersección de los tres.
Solución
Podemos proceder de manera escalonada. Primero, calculamos la intersección de A y B: los elementos comunes a ambos son 'c' y 'e', por lo que:
A ∩ B = {c, e}
A continuación, intersectamos este resultado con el conjunto C.
(A ∩ B) ∩ C = {c, e} ∩ {a, b, e, h}
De los elementos {c, e}, solo 'e' está presente en C. Por lo tanto, la intersección final de los tres conjuntos es el siguiente conjunto unitario:
A ∩ B ∩ C = {e}
Gráficamente la solución es:
Nota: debido a las propiedades de asociatividad y conmutatividad de la intersección, el orden en que calculamos las intersecciones no afecta el resultado. Así, podríamos haber primero calculado A ∩ C o B ∩ C y luego encontrar la intersección con el conjunto restante.
Ejemplo 5
Determinar la intersección de A = {1, 2, 4, 7}, B = {2, 3, 4, 5, 9} y C = {4, 5, 6, 7}.
Solución
Comenzamos encontrando los elementos que A y B tienen en común, que son 2 y 4:
A ∩ B = {2, 4}
Luego, buscamos los elementos de este nuevo conjunto que también pertenecen a C. De {2, 4}, solo el número 4 se encuentra en C. Así, la intersección de los tres conjuntos es:
A ∩ B ∩ C = {4}
Ejemplo 6
Sean los conjuntos M = {x ∈ N | x es múltiplo de 3 y x < 15} y N = {x ∈ N | x es par y x ≤ 12}. Encontrar M ∩ N.
Solución
Los conjuntos están dados por comprensión, así que primero los expresamos por extensión para identificar sus elementos.
El conjunto M está formado por los números naturales múltiplos de 3 y menores que 15:
M = {3, 6, 9, 12}
El conjunto N contiene los números naturales pares menores o iguales a 12:
N = {2, 4, 6, 8, 10, 12}
La intersección estará formada por los elementos comunes a ambos conjuntos. Los números que aparecen en M y en N son el 6 y el 12. Por lo tanto, la intersección es:
M ∩ N = {6, 12}
Propiedades
La operación de intersección en la teoría de conjuntos posee características esenciales que facilitan su manejo y cálculo.
1) Conmutatividad: el orden de los conjuntos no modifica el resultado.
A ∩ B = B ∩ A
2) Asociatividad: la agrupación de los conjuntos al intersectar no afecta el conjunto final.
(A ∩ B) ∩ C = A ∩ (B ∩ C)
3) Idempotencia: la intersección de un conjunto consigo mismo devuelve el mismo conjunto.
A ∩ A = A
4) Elemento identidad (o neutro): al intersectar cualquier conjunto con el conjunto universal, se obtiene el conjunto original.
A ∩ U = A
5) Propiedad de absorción: la intersección de cualquier conjunto con el conjunto vacío resulta en el conjunto vacío.
A ∩ ∅ = ∅
6) Distributividad respecto a la unión: la intersección se distribuye sobre la unión de conjuntos.
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
7) Ley de De Morgan: el complemento de una intersección equivale a la unión de los complementos.
(A ∩ B)’ = A’ ∪ B’
8) Cardinalidad: para conjuntos finitos, el tamaño de la intersección se relaciona con los tamaños individuales y su unión.
|A ∩ B| = |A| + |B| - |A ∪ B|
9) Relaciones con subconjuntos:
- Si un conjunto está contenido en otro, su intersección es el conjunto menor: si A ⊆ B, entonces A ∩ B = A.
- La intersección de dos conjuntos siempre es subconjunto de cada uno de ellos: A ∩ B ⊆ A y A ∩ B ⊆ B.
- Si dos conjuntos son subconjuntos de un tercero, su intersección también es subconjunto de él: si A ⊆ C y B ⊆ C, entonces A ∩ B ⊆ C
- Si un conjunto es subconjunto de otros dos, también lo es de su intersección: si X ⊆ A y X ⊆ B, entonces X ⊆ A ∩ B.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

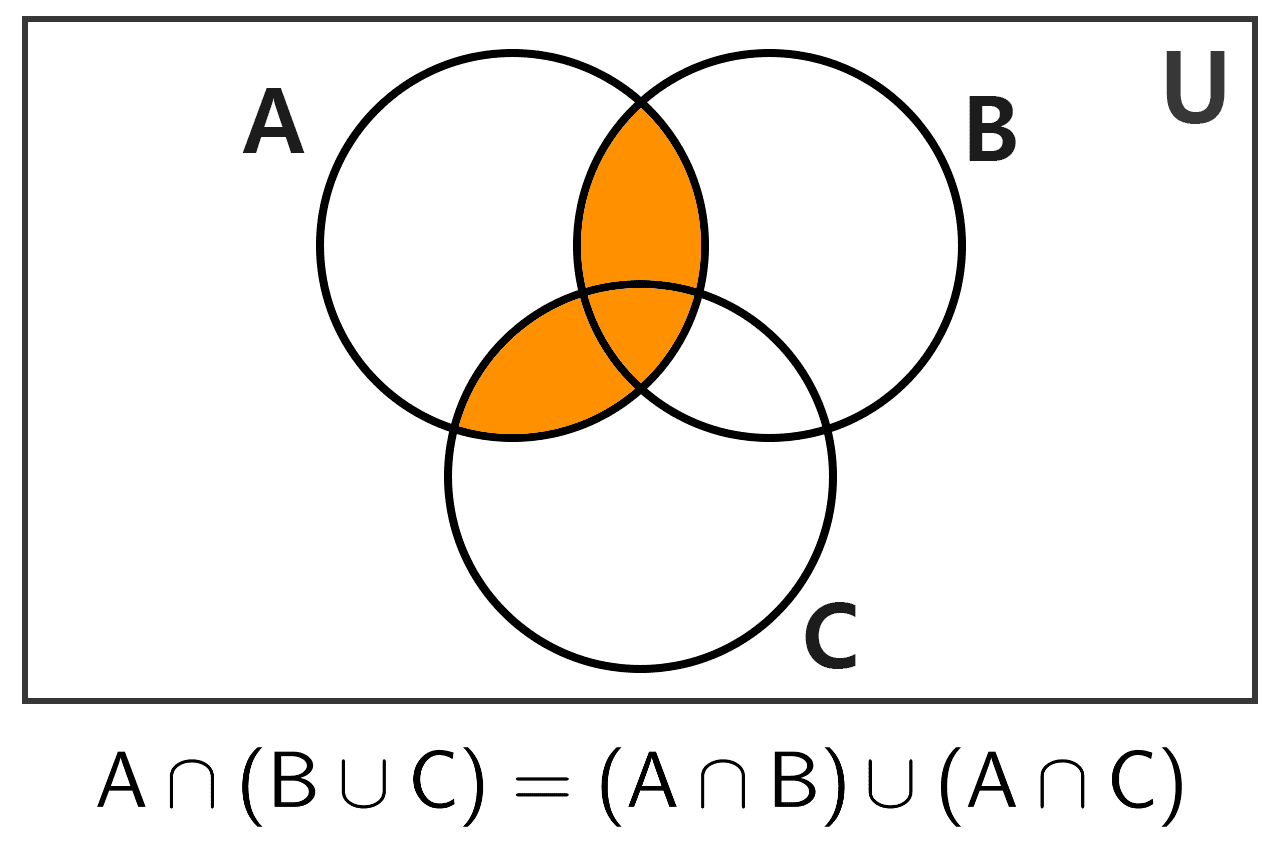
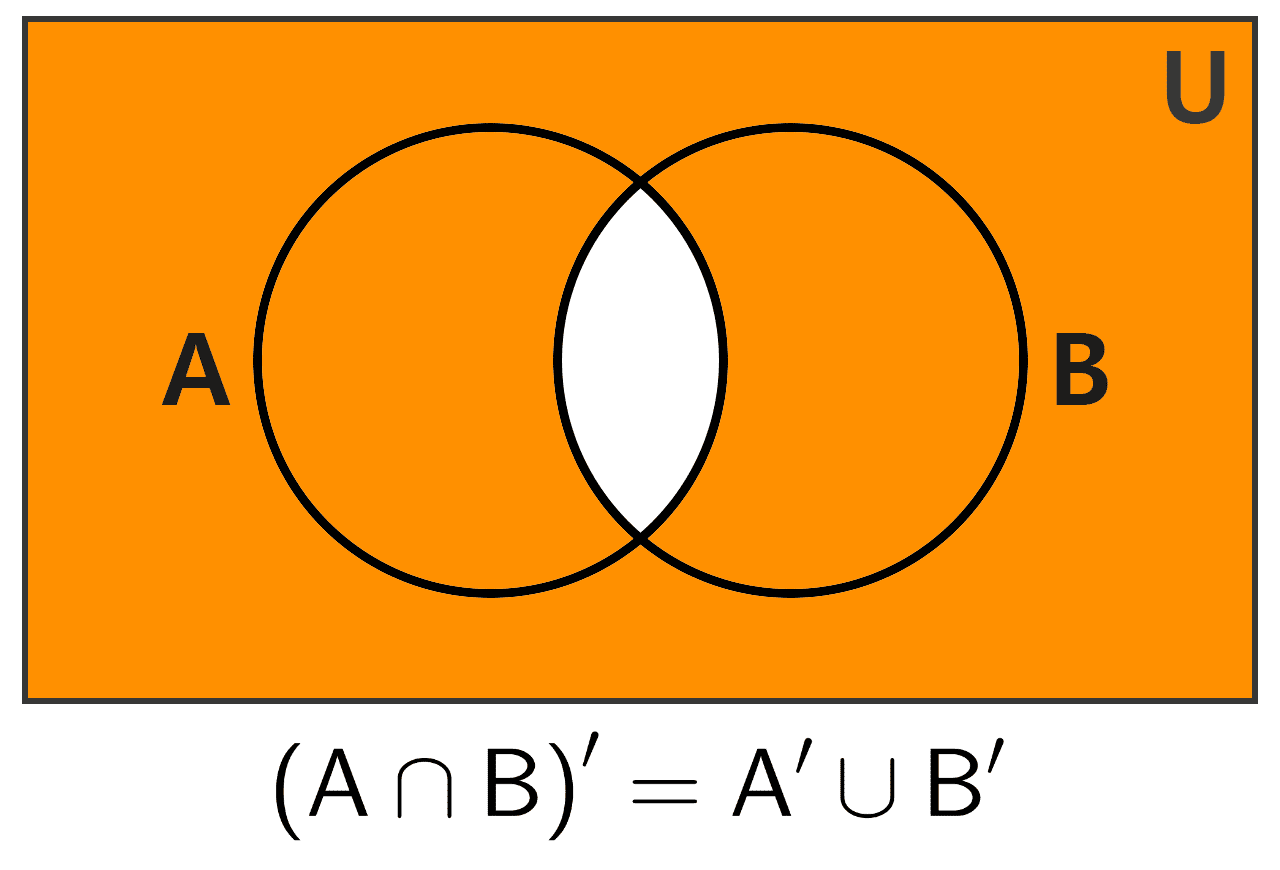
Otros artículos que te pueden interesar