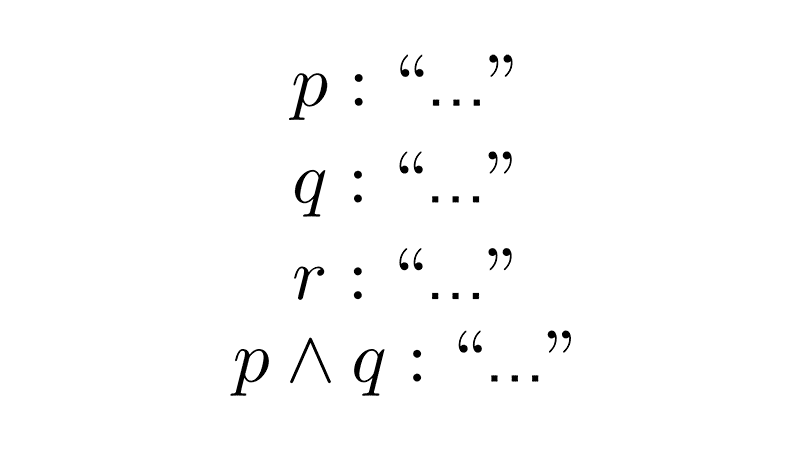
Lógica matemática
La lógica matemática es una disciplina centrada en el estudio y formalización del razonamiento mediante reglas y símbolos. Su objetivo principal es eliminar la ambigüedad del lenguaje natural para analizar la validez de los argumentos y determinar si están correctamente construidos.
Un argumento está correctamente construido cuando su conclusión se sigue necesariamente de sus premisas, es decir, si aceptamos que las premisas son verdaderas, la verdad de la conclusión está garantizada por la estructura del razonamiento. La lógica matemática proporciona el conjunto de reglas que nos permite derivar conclusiones válidas a partir de unas premisas dadas, lo que nos sirve para realizar demostraciones formales.
A diferencia de la lógica material o filosófica, que a menudo se interesa por la verdad concreta de las afirmaciones sobre el mundo, la lógica matemática se centra exclusivamente en la forma de los argumentos. Su objetivo no es determinar la verdad fáctica de una afirmación, sino establecer si, dada una estructura formal específica, la conclusión se deriva necesariamente. Esta abstracción del contenido permite el uso de símbolos para representar proposiciones y conectores, transformando argumentos lingüísticos en estructuras formales libres de ambigüedad.
El objetivo de este artículo es presentar una conceptualización de la lógica matemática que permita comprender su significado, su alcance y su función dentro del campo matemático. Para ello, estudiaremos sus ideas básicas, sus objetivos, ramas, tipos, y los elementos que la componen.
Índice
Objeto de estudio y propósito
El objeto de estudio principal de la lógica matemática son los sistemas formales y la inferencia válida. No estudia "cómo" piensa la mente humana (eso es psicología), sino la estructura de los argumentos para determinar si son correctos o incorrectos independientemente del contenido.
Sus objetivos fundamentales son los siguientes:
- Formalización del lenguaje: busca traducir el lenguaje natural y los argumentos matemáticos a un lenguaje simbólico exacto y sin ambigüedades. Este proceso define símbolos, reglas sintácticas para formar expresiones bien construidas y reglas semánticas para asignarles un valor de verdad, lo que permite analizar el esqueleto lógico de cualquier afirmación.
- Dar rigor a las demostraciones: proporciona un marco para distinguir una demostración correcta de una incorrecta. Al establecer un conjunto explícito de reglas de deducción, cualquier prueba puede ser descompuesta en pasos elementales y verificada, eliminando la dependencia de la intuición o el argumento persuasivo.
- Análisis de la computabilidad: un propósito más moderno de la lógica matemática es estudiar los fundamentos de la computación, un área ligada a la informática. Su objetivo es caracterizar de manera formal qué problemas son computables, es decir, cuáles pueden ser resueltos de manera efectiva por un algoritmo. Esto establece los límites teóricos de lo que una computadora puede o no calcular.
- Fundamentación de las matemáticas: uno de sus objetivos históricos, impulsado por figuras como Frege, Russell y Hilbert, ha sido cimentar toda la matemática sobre bases lógicas sólidas. Este programa buscaba demostrar que todas las verdades matemáticas podían derivarse de un conjunto pequeño y consistente de axiomas lógicos, utilizando únicamente las reglas de la lógica formal.
Nota: los teoremas de incompletitud de Kurt Gödel, publicados en 1931, demostraron límites fundamentales a los programas de fundamentación. Establecieron dos consecuencias fundamentales para cualquier sistema formal suficientemente complejo: primero, que es incompleto, ya que siempre habrá enunciados verdaderos que no pueden demostrarse dentro de él; y segundo, que no puede probar su propia consistencia, es decir, no puede garantizar internamente que no contiene contradicciones.
Ramas principales
La lógica matemática se organiza principalmente en cuatro grandes áreas de investigación: teoría de conjuntos, teoría de modelos, teoría de la demostración y teoría de la computabilidad.
Teoría de conjuntos
La teoría de conjuntos estudia las propiedades y relaciones de las colecciones abstractas de objetos, llamadas conjuntos, que sirven como fundamento para casi todas las ramas de las matemáticas. Los temas centrales incluyen las operaciones entre conjuntos, las relaciones de orden, los números cardinales y ordinales, y el estudio del infinito.
Su historia como disciplina matemática formal comenzó a finales del siglo XIX con el trabajo de Georg Cantor. Antes de él, el concepto de "infinito" era visto con recelo por los matemáticos, considerado una noción vaga y filosófica. Cantor, entre la década de 1870 y 1890, cambió este paradigma al tratar a los conjuntos infinitos como objetos completos que podían ser medidos y comparados.
Su aportación más célebre fue demostrar que no todos los infinitos son del mismo tamaño: mientras que el conjunto de los números naturales tiene un tamaño que denominó Aleph-cero (ℵ₀), el conjunto de los números reales es estrictamente mayor, un infinito "más denso" que no puede emparejarse uno a uno con los naturales. Este período se conoce como la teoría ingenua de conjuntos, donde se asumía que cualquier colección definible por una propiedad podía considerarse un conjunto.
Sin embargo, justo cuando las ideas de Cantor ganaban terreno, en 1901 el filósofo y matemático Bertrand Russell descubrió una paradoja devastadora para esta teoría ingenua. Si se permite formar un conjunto a partir de cualquier propiedad, se puede definir el "conjunto de todos los conjuntos que no se contienen a sí mismos". La pregunta de si este conjunto se contiene a sí mismo conduce a una contradicción lógica: si lo hace, entonces no cumple la propiedad para pertenecer a sí mismo, y si no lo hace, entonces sí cumple la propiedad y debe contenerse.
Para explicar su paradoja técnica, Russell usó esta analogía, conocida como la paradoja del barbero: "En un pueblo hay un barbero que afeita a todos los hombres que no se afeitan a sí mismos (y solo a esos)". La pregunta es: ¿se afeita el barbero a sí mismo? Si se afeita a sí mismo, entonces no puede afeitarse (porque solo afeita a los que no lo hacen); si no se afeita a sí mismo, entonces debe afeitarse (porque es su regla).
Para resolver esta crisis, los matemáticos se vieron obligados a abandonar la definición intuitiva y construir un sistema axiomático formal que evitara la formación de conjuntos paradójicos. Entre 1908 y los años 20, Ernst Zermelo y Abraham Fraenkel, con la contribución clave del axioma de elección, desarrollaron el sistema ZFC (Zermelo-Fraenkel con axioma de elección), que se convirtió en la base estándar aceptada.
Sus reglas, o axiomas, son un conjunto de principios que definen qué es un conjunto y qué operaciones están permitidas, prohibiendo la construcción demasiado amplia que llevaba a paradojas. Hay nueve axiomas, pero los que impiden las paradojas son:
- Axioma de especificación (o separación): establece que no puede crearse un conjunto simplemente definiendo una propiedad arbitraria. Para crear un conjunto nuevo, debe tomarse un conjunto ya existente y seleccionar (separar) de él los elementos que cumplen dicha propiedad. Si intentamos crear el "conjunto de todos los conjuntos que no se contienen a sí mismos", ZFC pregunta: "¿de qué conjunto padre se están sacando estos elementos?". Como no existe un "conjunto de todo el universo" (prohibido por ZFC), no puede formarse la paradoja de Rusell.
- Axioma de regularidad (o fundación): impide que un conjunto se contenga a sí mismo, eliminando círculos viciosos y las muñecas rusas infinitas hacia adentro. Esto elimina de raíz la posibilidad de preguntar "¿se contiene este conjunto a sí mismo?", porque la respuesta por definición en ZFC siempre es negativa.
Una vez consolidado este sistema, surgió un descubrimiento profundo: existen preguntas fundamentales sobre los conjuntos que el propio sistema ZFC no puede responder. El ejemplo más famoso es la hipótesis del continuo, formulada por Cantor, que pregunta si existe un tamaño infinito estrictamente mayor que el de los naturales pero menor que el de los reales.
Kurt Gödel demostró en 1940 que la hipótesis no podía refutarse desde ZFC, y Paul Cohen probó en 1963 que tampoco podía probarse. Esto la convierte en una proposición indecidible dentro del sistema estándar: se puede añadir como un axioma adicional o negarla, y en ambos casos se obtiene una matemática consistente pero diferente.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
0,0 / 5 — 0 votos
Teoría de modelos
La teoría de modelos estudia la relación entre los lenguajes formales, con sus reglas de construcción y demostración (sintaxis), y las estructuras matemáticas que los interpretan y les dan significado (semántica). Los temas centrales incluyen la definición de verdad matemática, la consistencia, la completitud de las teorías, y el estudio de qué estructuras pueden satisfacer un conjunto dado de reglas o axiomas.
La sintaxis se refiere a la parte puramente formal de un lenguaje: sus símbolos, las reglas para construir fórmulas bien formadas y las reglas de inferencia para derivar teoremas a partir de axiomas, sin asignar ningún significado a los símbolos. Por ejemplo, en la aritmética, la sintaxis nos permite escribir la expresión "∀x (x + 0 = x)" como una cadena de símbolos válida.
La semántica, en cambio, proporciona la interpretación: asigna significados a esos símbolos dentro de una estructura concreta. La misma fórmula "∀x (x + 0 = x)" se interpreta en la estructura de los números naturales como la afirmación de que sumar cero a cualquier número da el mismo número, lo que resulta ser una afirmación verdadera en esa interpretación.
Su desarrollo moderno se consolidó en el siglo XX, estrechamente vinculado a los trabajos de Kurt Gödel sobre completitud e incompletitud, y de Alfred Tarski, quien formalizó una definición rigurosa de la verdad en un lenguaje formal dentro de una estructura.
Un ejemplo clásico es la teoría de grupos, definida por unos pocos axiomas (asociatividad, elemento neutro, elemento inverso). La semántica de esta teoría son sus modelos concretos: el conjunto de los enteros con la suma o los números reales no nulos con la multiplicación. La teoría de modelos estudia qué propiedades son comunes a todos estos modelos y cuáles los distinguen.
Un resultado importante es el teorema de completitud de Gödel, que establece un puente entre sintaxis y semántica: afirma que una fórmula es demostrable a partir de los axiomas (consecuencia sintáctica) si y sólo si es verdadera en todos los modelos que satisfacen dichos axiomas (consecuencia semántica).
Otro pilar es el teorema de compacidad, que implica, por ejemplo, que si una teoría tiene modelos arbitrariamente grandes, entonces debe tener también un modelo infinito. Este teorema tiene consecuencias profundas, como la imposibilidad de caracterizar la finitud mediante un conjunto de axiomas de primer orden.
Al igual que ocurrió con la teoría de conjuntos, la teoría de modelos también enfrenta límites inherentes. Los teoremas de incompletitud de Gödel muestran que teorías suficientemente expresivas, como la aritmética, poseen enunciados que no pueden probarse ni refutarse desde sus axiomas. Desde la perspectiva de la teoría de modelos, esto significa que existen modelos no estándar de la aritmética: estructuras que satisfacen todos los axiomas de Peano pero que contienen elementos "infinitos" más allá de los números naturales usuales.
Teoría de la demostración (o de la prueba)
La teoría de la demostración estudia las demostraciones como objetos matemáticos formales. Se centra en la estructura, propiedades y limitaciones de los sistemas deductivos (sintaxis), analizando qué significa probar un teorema a partir de axiomas mediante reglas de inferencia. Sus temas principales incluyen el análisis de la consistencia, la fuerza relativa de diferentes sistemas formales, la normalización de demostraciones y los límites de la derivabilidad.
Mientras la teoría de modelos conecta la sintaxis con interpretaciones en estructuras (semántica), la teoría de la demostración se ocupa casi exclusivamente del lado sintáctico. Su objeto de estudio no es la "verdad" en un modelo, sino la noción de "demostrabilidad" dentro de un cálculo. Bajo esta teoría, una demostración formal es una secuencia finita de fórmulas, donde cada paso es un axioma o se deriva de pasos anteriores mediante una regla aplicada.
Su origen como disciplina autónoma se sitúa en el programa de Hilbert de principios del siglo XX, cuyo objetivo era fundamentar las matemáticas demostrando que sistemas formales como la aritmética eran consistentes y completos. Este programa buscaba, en cierto modo, "demostrar" la seguridad de las matemáticas usando solo herramientas combinatorias sobre las propias demostraciones.
Sin embargo, los teoremas de incompletitud de Gödel en 1931 asestaron un golpe decisivo a este plan, al probar que cualquier sistema formal suficientemente rico para contener la aritmética básica no puede demostrar su propia consistencia, y que siempre existirán enunciados verdaderos indemostrables dentro del sistema.
Más allá de este resultado negativo, la teoría de la demostración floreció con contribuciones profundas. Gerhard Gentzen, para probar la consistencia de la aritmética (usando métodos más fuertes que los permitidos por Hilbert), introdujo el cálculo de secuentes y el teorema de eliminación del corte. Este último asegura que cualquier teorema puede demostrarse analizando únicamente los conceptos que aparecen en su propio enunciado, sin necesidad de inventar conceptos externos.
Teoría de la computabilidad (o de la recursión)
La teoría de la computabilidad estudia los límites fundamentales de lo que puede ser calculado o decidido por un procedimiento mecánico efectivo. Sus temas centrales incluyen la definición formal de algoritmo, la clasificación de problemas en decidibles (solubles por un algoritmo) e indecidibles (no solubles), y el estudio de la jerarquía de complejidad entre problemas computables.
Su origen histórico está profundamente ligado al problema de decisión planteado por David Hilbert en 1928, que preguntaba si existe un procedimiento algorítmico universal (algo así como una "receta" mecánica) para determinar la verdad o falsedad de cualquier enunciado matemático formal. La búsqueda de una respuesta llevó a la formalización del concepto intuitivo de "algoritmo".
Esta búsqueda culminó en la década de 1930 con trabajos equivalentes de Alonzo Church (con el cálculo lambda) y, de forma especialmente influyente, de Alan Turing. Este último propuso en 1936 un modelo abstracto y minimalista de computación: la máquina de Turing. Esta máquina consta de una cinta infinita dividida en celdas, un cabezal que lee y escribe símbolos, y un conjunto finito de reglas (el programa) que dictan su comportamiento en función del símbolo leído y un estado interno.
A pesar de su simplicidad, la tesis de Church-Turing postula que cualquier función computable de manera intuitiva puede ser calculada por una máquina de Turing, estableciendo este modelo como el estándar para definir qué es computable. Un problema se considera decidible si existe una máquina de Turing que, para cualquier entrada del problema, siempre se detiene (se para) y da la respuesta correcta "sí" o "no".
Los resultados finales de esta teoría definen las fronteras de la matemática algorítmica. El corazón de este límite es el problema de la parada, que plantea una pregunta aparentemente sencilla: dado un programa (o una máquina de Turing) y una entrada concreta para él, ¿es posible diseñar un algoritmo general que determine, sin ejecutarlo, si ese programa terminará su ejecución en un tiempo finito o si, por el contrario, caerá en un bucle y nunca se detendrá?
Turing utilizó su propio modelo para resolver negativamente el problema de decisión de Hilbert: demostró que el problema de la parada es indecidible. Esto significa que no existe (ni puede existir jamás) un programa que analice cualquier otro código y decida infaliblemente, en todos los casos posibles, si este se detendrá o se quedará en un bucle infinito.
Para explicar este límite, se usa un razonamiento de autorreferencia similar a la paradoja de Russell: si existiera tal máquina "analizadora", podríamos construir un programa tramposo que haga exactamente lo contrario de lo que predice el analizador (si el analizador dice que parará, el programa entra en bucle; si dice que no parará, el programa se detiene), generando una contradicción.
Este resultado fue profundo: demostró que hay problemas matemáticos perfectamente definidos que son indecidibles. La ignorancia en matemáticas no es temporal, en algunos casos es estructural: hay verdades que una máquina nunca podrá alcanzar.
Tipos de lógica
Los tipos de lógica se refieren a los diferentes sistemas formales desarrollados para estudiar la estructura y validez del razonamiento. Tradicionalmente, se dividen en dos grandes categorías: la lógica clásica (o estándar), que es la base de las matemáticas convencionales, y las lógicas no clásicas, que amplían o modifican sus principios fundamentales para abordar contextos más específicos.
Lógica clásica
La lógica clásica es el sistema de razonamiento formal, base de las matemáticas tradicionales, que define las reglas para determinar la validez de un argumento a partir de principios fundamentales que rigen el comportamiento de la verdad y la falsedad.
Sus principios fundamentales son:
- Principio de bivalencia: toda proposición tiene exactamente uno de dos valores de verdad: es verdadera (V) o es falsa (F). No admite un tercer valor o un estado intermedio.
- Principio de no contradicción: una proposición y su negación no pueden ser verdaderas simultáneamente. Formalmente, para cualquier proposición p, es falso que p y no-p sean ciertas a la vez: ¬(p ∧ ¬p).
- Principio del tercero excluido: para cualquier proposición, o bien ella es verdadera, o bien su negación lo es. No existe una tercera posibilidad. Su fórmula es p ∨ ¬p.
- Principio de monotonicidad: si una conclusión se deduce válidamente de un conjunto de premisas, añadir nuevas premisas nunca invalidará esa conclusión.
La lógica clásica se divide a su vez en distintos órdenes: lógica proposicional, lógica de predicados y lógicas de orden superior.
Lógica proposicional (orden cero)
La lógica proposicional, también llamada lógica de enunciados o cálculo proposicional, tiene como objeto de estudio a las proposiciones: afirmaciones declarativas completas que pueden ser calificadas inequívocamente como verdaderas (V) o falsas (F), según el principio de bivalencia.
Algunos ejemplos de proposiciones son:
- "El cielo es azul" (verdadero)
- "2 + 2 = 4" (verdadero)
- "3 es un número par" (falso)
La clave de este sistema radica en que no analiza la estructura interna de estas proposiciones, sino que las toma como bloques atómicos indivisibles y se centra en cómo su valor de verdad se ve afectado al combinarlas mediante conectores lógicos.
Los elementos fundamentales de este cálculo son las variables proposicionales (generalmente denotadas con letras como p, q, r), que representan proposiciones atómicas. La potencia del sistema surge con los conectivos lógicos, que permiten construir proposiciones compuestas (o moleculares) a partir de las atómicas.
Los conectivos lógicos fundamentales son:
- Negación (¬): invierte el valor de verdad de una proposición.
- Conjunción (∧): es verdadera solo si ambas proposiciones unidas son verdaderas.
- Disyunción (∨): es verdadera si al menos una de las dos proposiciones es verdadera (es inclusiva).
- Condicional (→): expresa una implicación; solo es falsa cuando el antecedente es verdadero y el consecuente falso.
- Bicondicional (↔): es verdadero cuando ambas proposiciones tienen exactamente el mismo valor de verdad.
Ejemplo
Sean p: "El cielo es azul", q: "2 + 2 = 4" y r: "3 es un número par", las siguientes son algunas de las proposiciones moleculares que podemos formar:
¬p: "El cielo no es azul"
q ∧ r: "2+2=4 y 3 es un número par"
p ∨ q: "El cielo es azul o 2 + 2 = 4"
p → q: "Si el cielo es azul, entonces 2 + 2 = 4"
q ↔ r: "2 + 2 = 4 si y sólo si 3 es un número par"
Para determinar el valor de verdad de una proposición compuesta, se construye su tabla de verdad. Este método considera todas las posibles combinaciones de verdad (V) o falsedad (F) para las proposiciones atómicas que la componen. Al hacer esto, podemos clasificarla en una de tres categorías fundamentales: tautología (verdadera en todos los casos posibles), contingencia (verdadera en algunos casos y falsa en otros) o contradicción (falsa en todos los casos posibles).
El objetivo central de la lógica proposicional es determinar la validez de los argumentos. Un argumento es una secuencia de proposiciones donde las premisas conducen a una conclusión. Se dice que es válido si, y sólo si, en todos los casos en que todas las premisas son verdaderas, la conclusión también lo es.
Algunos ejemplos de razonamientos válidos son:
- Si llueve, entonces el suelo está mojado. Está lloviendo, por lo tanto, el suelo está mojado.
- Si hay luz solar, entonces es de día. No es de día, por lo tanto, no hay luz solar.
- Si no suena el despertador, me despierto tarde. Si me despierto tarde, pierdo el autobús. Por lo tanto, si no suena el despertador, pierdo el autobús.
El primer caso corresponde a una regla de inferencia llamada modus ponens, el segundo a un modus tollens y el tercero a un silogismo hipotético. Sus estructuras formales son las siguientes:
- Modus Ponens: [(p → q) ∧ p] → q
- Modus Tollens: [(p → q) ∧ ¬q] → ¬p
- Silogismo hipotético: [(p → q) ∧ (q → r)] → (p → r)
A pesar de su poder para analizar la validez de argumentos basados en la conexión de proposiciones completas, la lógica proposicional tiene una limitación fundamental: no puede analizar la estructura interna de las oraciones. Para este sistema, cada afirmación es un bloque atómico e indivisible; no comprende conceptos como sujetos, predicados, cuantificadores ni relaciones entre individuos.
Por ejemplo, ante las afirmaciones "todos los hombres son mortales" y "Sócrates es hombre", la lógica proposicional sólo vería dos proposiciones simples y distintas. Al carecer de herramientas para descomponerlas y ver que "Sócrates" es un caso particular del sujeto "hombres", es incapaz de deducir la conclusión "Sócrates es mortal".
En este nivel, las premisas son hechos desconectados. Para superar esta barrera y poder formalizar razonamientos que dependen de la estructura interna y de los cuantificadores ("todos", "algún", "ningún") es que se desarrollan sistemas más potentes, como la lógica de predicados.
Lógica de predicados (o de primer orden)
La lógica de predicados es un sistema formal que extiende la lógica proposicional al permitir analizar la estructura interna de los enunciados, distinguiendo sujetos y predicados para poder razonar sobre propiedades, relaciones y cuantificaciones ("todos" o "algunos") sobre objetos de un dominio.
Mientras que la lógica proposicional trata las proposiciones como átomos indivisibles (p, q, r), la lógica de predicados las descompone introduciendo los siguientes elementos:
- Términos: representan objetos específicos dentro de un dominio. Pueden ser constantes (como a, b, s), que denotan individuos particulares (por ejemplo, s para Sócrates), o variables (como x, y), que actúan como marcadores de posición.
- Predicados: denotan propiedades de un objeto o relaciones entre varios objetos. Se simbolizan con letras mayúsculas (como M para "ser mortal") y se aplican a los términos. Por ejemplo, "Sócrates es mortal" se analiza como M(s), donde M es un predicado.
- Funciones proposicionales: son expresiones como G(x): "x es griego", que contienen variables y se convierten en una proposición con valor de verdad definido cuando dichas variables son sustituidas por términos específicos o la expresión se cuantifica.
Para convertir funciones proposicionales en proposiciones se utilizan cuantificadores. El cuantificador universal (∀) afirma "para todo x", mientras que el cuantificador existencial (∃) afirma "existe al menos un x".
Esto permite formalizar enunciados como:
- ∀x: G(x): "para todo x, x es griego" o "Todos son griegos".
- ∃x/ G(x): "existe al menos un x tal que x es griego" o "Alguno es griego".
- ∀n ∈ N, ∃m ∈ N / (m = n+1): "Para todo número natural n, existe un número natural m tal que m es el siguiente de n", es decir, "todo número natural tiene un sucesor".
Una regla de inferencia fundamental es la especificación universal: si una propiedad es verdadera para todos los elementos de un dominio, entonces es verdadera para uno particular elegido de ese dominio. Formalmente, de ∀x P(x) se deduce P(a), donde a es una constante específica. Por ejemplo, de la premisa "todos los hombres son mortales", se puede deducir que "Sócrates es mortal", siempre que se sepa que Sócrates es un hombre.
Esta y otras reglas son las herramientas que permiten "quitar" los cuantificadores para trabajar con fórmulas simples donde podemos aplicar las reglas de inferencia de la lógica proposicional.
Otras reglas de inferencia de la lógica de predicados son:
- La generalización existencial: si una propiedad es cierta para un individuo concreto o para una constante específica, entonces se puede afirmar que existe al menos un elemento para el cual esa propiedad es verdadera. Formalmente, de P(a) se deduce ∃x P(x). Por ejemplo, si sabemos que "Platón es filósofo", podemos concluir que "existe al menos un filósofo".
- La generalización universal: si se puede demostrar que una propiedad P es cierta para un elemento arbitrario c (es decir, sin hacer suposiciones especiales sobre él), entonces se puede concluir que P es cierta para todo x: P(c) implica ∀x P(x). Por ejemplo, si al tomar un triángulo cualquiera se demuestra que la suma de sus ángulos es 180°, entonces se concluye que esto vale para todos los triángulos.
Importante: la generalización universal no permite concluir que una propiedad es universal solo por probarla en un caso particular. Para aplicarla correctamente, el elemento sobre el que se prueba la propiedad debe ser completamente arbitrario y representativo del dominio, sin características especiales. Por ejemplo, de probar que "un gato llamado Garfield es anaranjado" no se puede deducir que "todos los gatos son anaranjados", porque Garfield es un caso específico.
Lógica de segundo orden (órden superior)
La lógica de segundo orden es una extensión de la lógica de predicados que permite cuantificar no solo sobre objetos individuales (como personas o números), sino también sobre propiedades, funciones y conjuntos.
Esto significa que, mientras en la lógica de primer orden los cuantificadores solo se aplican a variables que representan elementos del dominio, en el segundo orden podemos cuantificar sobre variables que representan predicados o conjuntos, permitiendo expresar afirmaciones sobre propiedades en sí mismas.
Por ejemplo, en primer orden podríamos decir "para todo x, x es rojo", pero en segundo orden podemos afirmar "existe una propiedad P tal que para todo x, P(x) es verdadero", donde P deja de ser un símbolo fijo y se convierte en una variable sobre la que podemos cuantificar. Esta capacidad de cuantificar sobre propiedades y conjuntos nos permite formalizar conceptos matemáticos más complejos que no pueden expresarse completamente en primer orden.
Un ejemplo central es el principio de inducción matemática, que puede enunciarse así: para cualquier propiedad P de los números naturales, si P(0) es verdadera y siempre que P(n) sea verdadera implica P(n+1), entonces para todo número natural n, P(n) es verdadera. Formalmente, se expresa como ∀P [(P(0) ∧ ∀n (P(n) → P(n+1))) → ∀n P(n)], donde P es una variable que representa cualquier propiedad.
Nota: existen lógicas de órdenes aún más altos, como la lógica de tercer orden, que permite cuantificar no solo sobre propiedades de objetos (como en segundo orden), sino también sobre propiedades de propiedades. Sin embargo, estos sistemas rara vez se aplican fuera de contextos teóricos muy específicos debido a su complejidad semántica y deductiva.
Lógicas no clásicas
Anteriormente mencionamos que la lógica clásica se basa en principios fundamentales como el de bivalencia, no contradicción, tercero excluido y monotonía. Se considera que una lógica es no clásica cuando rechaza o modifica al menos uno de estos pilares, abriendo camino a sistemas de razonamiento que abordan matices y contextos que la lógica tradicional no puede capturar completamente.
Entre las principales lógicas no clásicas se encuentran:
- Lógicas multivaluadas: estas lógicas rechazan el principio de bivalencia al admitir más de dos valores de verdad. Un ejemplo clásico es la lógica trivalente de Łukasiewicz, que además de "verdadero" y "falso" introduce un tercer valor, como "intermedio" o "posible", para representar situaciones de indeterminación que no pueden reducirse a una simple dualidad.
- Lógica difusa (Fuzzy logic): también rechaza la bivalencia, pero lo hace de forma continua al establecer un espectro infinito de valores de verdad entre 0 (completamente falso) y 1 (completamente verdadero). A diferencia de las lógicas multivaluadas, que definen un conjunto discreto de "casillas" de verdad, la lógica difusa opera con grados. Un ejemplo práctico se encuentra en un aire acondicionado inteligente: en lugar de encenderse al 100% o apagarse por completo según un umbral fijo, evalúa grados como "hace un poco de calor" y modula su potencia al 20% o 80% de forma proporcional a la temperatura.
- Lógica intuicionista: esta lógica rechaza específicamente el principio del tercero excluido, sosteniendo que para afirmar que una proposición es verdadera no basta con demostrar que su negación es falsa; se requiere una prueba constructiva o evidencia directa. Por ejemplo, no es suficiente argumentar "no es cierto que no esté lloviendo" para concluir "está lloviendo"; se necesita una prueba positiva, como observar las gotas de agua, para establecer la verdad de la afirmación.
- Lógica paraconsistente: rechaza el principio de no contradicción en su forma absoluta y, crucialmente, evita el principio de explosión, que en la lógica clásica permite derivar cualquier conclusión a partir de una contradicción. Las lógicas paraconsistentes permiten aislar y contener contradicciones locales sin que el sistema de razonamiento colapse. Esto es útil en bases de datos o sistemas de sensores donde pueden coexistir datos contradictorios (por ejemplo, un sensor registra 20°C y otro 25°C para la misma medición) sin invalidar todo el conocimiento del sistema.
- Lógicas no monotónicas: estas rechazan el principio de monotonicidad, aceptando que al agregar nueva información se pueden invalidar conclusiones anteriores. Así, el razonamiento se vuelve provisional y revisable. Un ejemplo clásico es la regla "todas las aves vuelan", que permite concluir que un pájaro específico vuela; sin embargo, al descubrir que ese pájaro es un pingüino, la conclusión se retracta. Este tipo de lógica es fundamental en sistemas como los de diagnóstico médico, donde un síntoma nuevo puede cambiar por completo la hipótesis inicial.
- Lógica modal: constituye un caso especial, ya que generalmente no rechaza los principios clásicos, pero amplía la semántica al introducir operadores como "es posible que" (◇) y "es necesario que" (□). Este añadido formal cambia el alcance de la verdad, considerándola no como un hecho absoluto sino en relación con modos o contextos, lo cual la clasifica como no clásica. Permite razonar sobre futuros hipotéticos, riesgos o conocimiento, diferenciando, por ejemplo, entre "es posible que el paciente tenga gripe" (basado en algunos síntomas) y "es necesario que el paciente tenga gripe" (con base en un cuadro clínico inequívoco).
Bibliografía consultada
- Acevedo González, G. (2011). Lógica Matemática. Universidad Nacional Abierta y a Distancia (UNAD).
- Castillo P, E. y Pinta, M. (2015). Lógica Matemática I: Proposiciones y Leyes de Inferencia (2.ª edición). Universidad Técnica de Machala.
- Copi, I. y Cohen, C. (2013). Introducción a la Lógica (2.ª edición). Limusa.
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
- Garrido, M. (1974). Lógica simbólica (4.ª edición). Tecnos.
- Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
- Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
Contenidos de lógica matemática
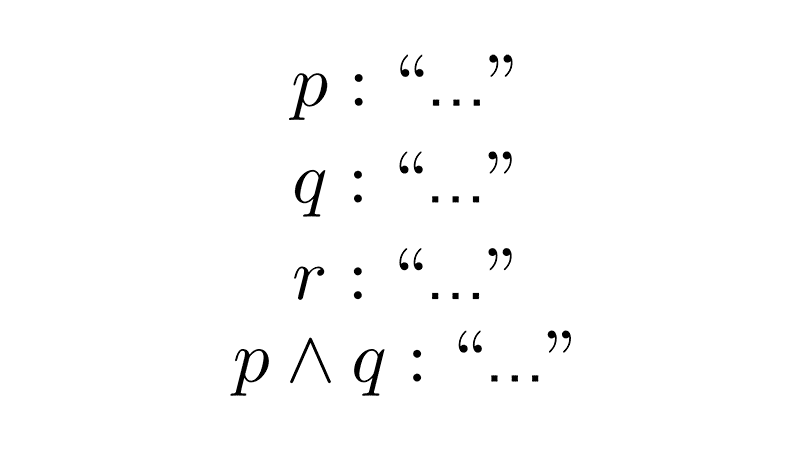
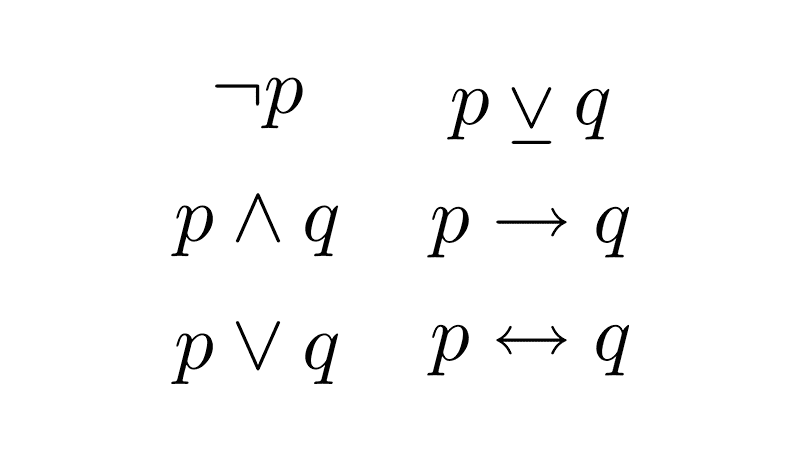
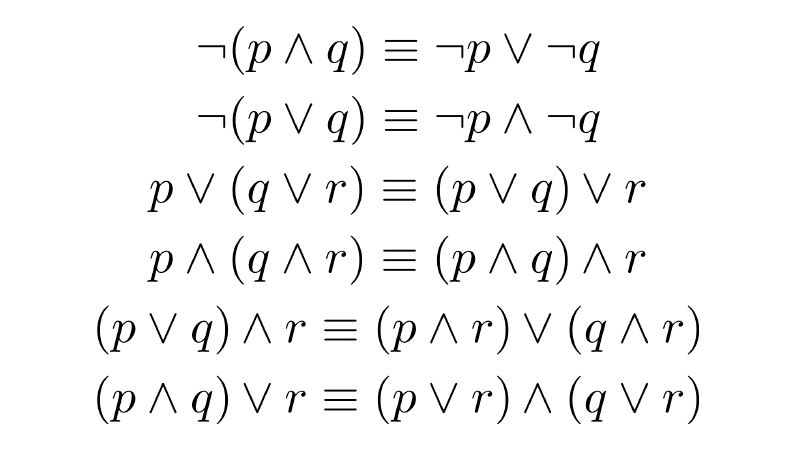
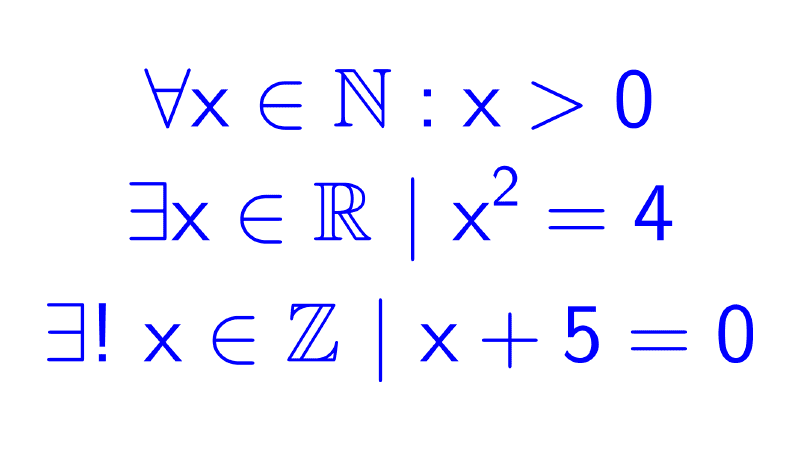
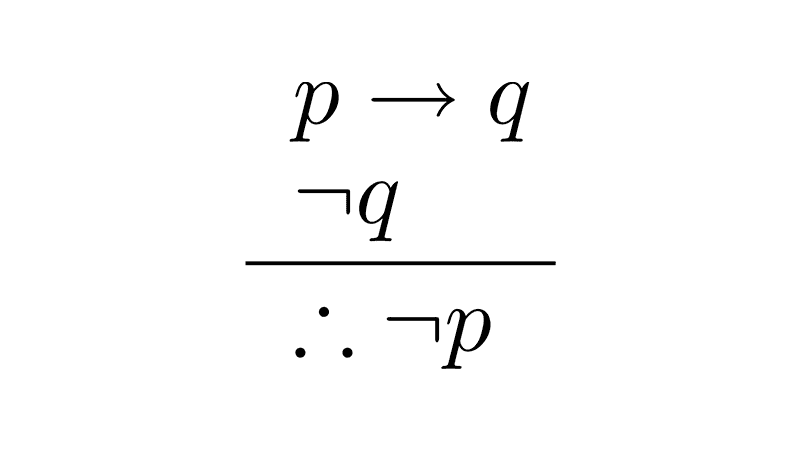
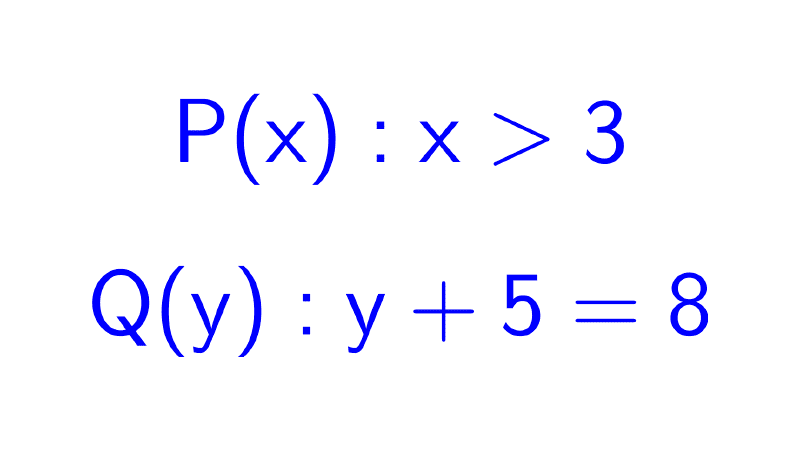



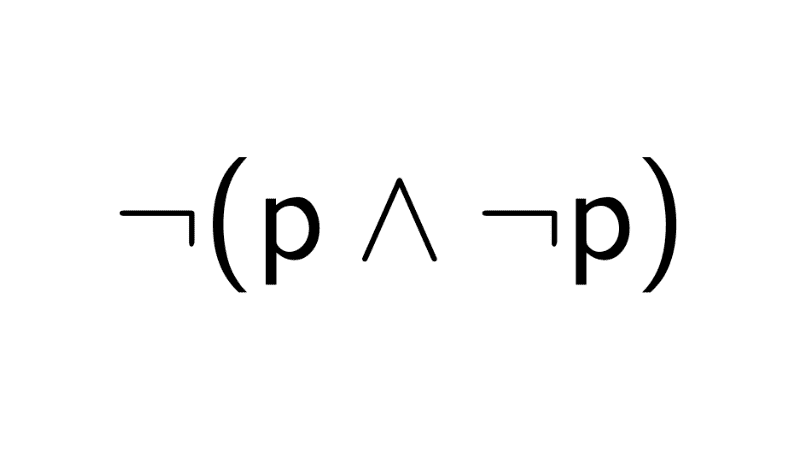
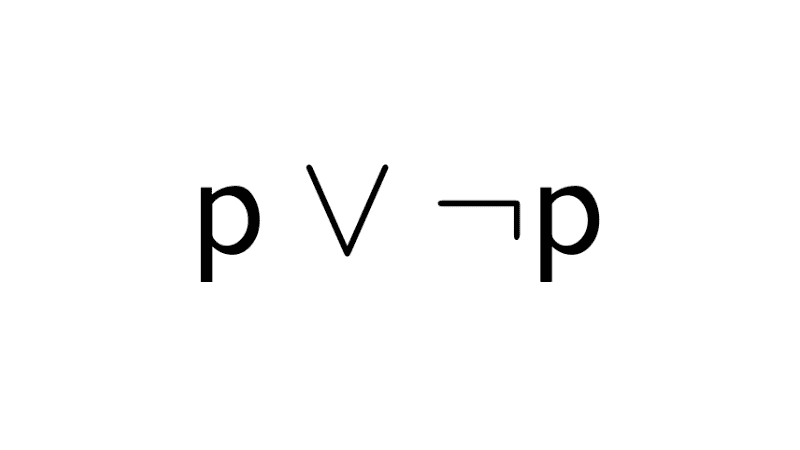

¿Te ha servido este contenido? ¡Califícalo!
0,0 / 5 — 0 votos
CÓMO CITAR ESTE ARTÍCULO
Machado, D. (2025, 24 de diciembre). Lógica matemática. Flamath. https://es.flamath.com/logica-matematica

Deja una respuesta