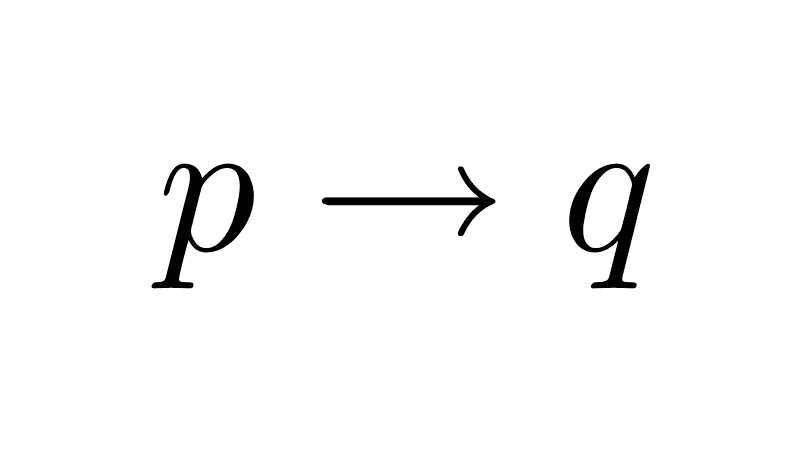
Bicondicional lógico
El bicondicional, también conocido como doble implicación, es un conectivo lógico que enlaza dos proposiciones para formar una nueva la cual es verdadera cuando las proposiciones originales tienen el mismo valor de verdad (ambas verdaderas o ambas falsas), y es falsa en caso contrario. Se representa con los símbolos “↔” o “⇔” y se lee como “si y solo si”.
Algunos ejemplos del uso del bicondicional son:
- "Un triángulo es equilátero si y sólo si sus tres ángulos internos son iguales". Esta proposición compuesta es verdadera porque ambas condiciones, tener lados iguales y ángulos iguales, son equivalentes en un triángulo.
- En la expresión “aprobaré si y solo si estudio para el examen", el bicondicional establece una doble condición: estudiar es necesario y suficiente para aprobar, y aprobar implica que he estudiado. Si estudio y apruebo, es verdadera; si no estudio y apruebo de todos modos, es falsa (al igual que si estudio y no apruebo).
- "Puedes ingresar al concierto si y solo si tienes una entrada" es verdadero sólo en dos casos: si tienes entrada y puedes entrar, o si no tienes entrada y no puedes entrar. La oración se vuelve falsa si, por ejemplo, tienes una entrada pero no te permiten ingresar.
Índice
Tabla de verdad
Como dijimos, el bicondicional es verdadero únicamente cuando las dos proposiciones que conecta poseen el mismo valor de verdad (ambas verdaderas o ambas falsas), y es falso cuando los valores de verdad son distintos (una verdadera y otra falsa). Esto queda claro al analizar su tabla de verdad:
| p | q | p ↔ q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | V |
Existen diferentes formas de leer la proposición bicondicional p ↔ q, todas ellas equivalentes en significado. Algunas de las más comunes son:
- p si y sólo si q.
- p es equivalente a q.
- p es una condición necesaria y suficiente para q.
- Si p, entonces q, y si q, entonces p.
- q si y sólo si p.
De manera abreviada, la expresión "si y sólo si" suele escribirse como "sii". El bicondicional tiene una estrecha relación con las equivalencias lógicas: si A y B son dos fórmulas proposicionales y la proposición A ↔ B es siempre verdadera (una tautología), entonces decimos que A y B son lógicamente equivalentes y lo simbolizamos como A ≡ B.
Es importante no confundir entre el bicondicional (↔) y el condicional simple (→). Mientras que el condicional establece que una proposición es condición suficiente para la otra (si p, entonces q), el bicondicional afirma una relación mutua de necesidad y suficiencia: p es condición necesaria y suficiente para q, y viceversa.
Por ejemplo, la proposición "si un número es divisible por 4, entonces es par" es un condicional verdadero: ser divisible por 4 es una condición suficiente para ser par. Si intentamos convertirla en un bicondicional: "un número es divisible por 4 si y sólo si es par", la proposición se vuelve falsa. La razón es que el bicondicional exige que la condición también funcione a la inversa.
En este caso, no es cierto que "si un número es par, entonces es divisible por 4" (pensemos en el número 6, que es par pero no es divisible por 4). Por lo tanto, ser par no es una condición suficiente para ser divisible por 4, lo que rompe la equivalencia exigida por el bicondicional.
Propiedades
El coimplicador posee una serie de propiedades lógicas fundamentales que veremos a continuación.
1) Equivalencia a una conjunción de condicionales: la propiedad esencial del bicondicional es que es lógicamente equivalente a la conjunción de dos condicionales dirigidos en sentidos opuestos (un condicional y su recíproco).
p ↔ q ≡ (p → q) ∧ (q → p)
Esto significa que afirmar "p si y sólo si q" es lo mismo que afirmar "si p, entonces q" y "si q, entonces p" de manera simultánea.
2) Definición con conjunción y disyunción: la doble implicación también puede definirse utilizando los conectivos de conjunción y disyunción.
p ↔ q ≡ (p ∧ q) ∨ (¬p ∧ ¬q)
Nótese que es equivalente a afirmar que ambas proposiciones son verdaderas o que ambas son falsas.
3) Propiedad de identidad: toda proposición es equivalente a sí misma, esta es una propiedad fundamental.
p ↔ p
4) Propiedad conmutativa: el orden de las proposiciones en un bicondicional no altera su valor de verdad.
p ↔ q ≡ q ↔ p
5) Propiedad transitiva: si una proposición es equivalente a una segunda, y esta segunda es equivalente a una tercera, entonces la primera y la tercera también son equivalentes.
Si (p ↔ q) y (q ↔ r) son verdaderas, entonces (p ↔ r) también es verdadera.
6) Propiedad asociativa: cuando se enlazan múltiples coimplicadores, la forma de agruparlos no cambia el resultado.
(p ↔ q) ↔ r ≡ p ↔ (q ↔ r)
7) Relación con la disyunción exclusiva: el bicondicional y la disyunción exclusiva (⊻) son negaciones lógicas entre sí. Mientras el bicondicional es verdadero cuando los valores coinciden, la disyunción exclusiva es verdadera cuando los valores son diferentes.
(p ↔ q) ≡ ¬(p ⊻ q)
8) Negación de un bicondicional: negar una equivalencia significa afirmar que las proposiciones tienen valores de verdad distintos; esto es, precisamente, la definición de la disyunción exclusiva.
¬(p ↔ q) ≡ (p ⊻ q) ≡ (p ∧ ¬q) ∨ (¬p ∧ q)
9) Contraposición del bicondicional: al igual que con el condicional simple, el doble implicador tiene una forma contrapositiva válida.
(p ↔ q) ≡ (¬q ↔ ¬p)
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

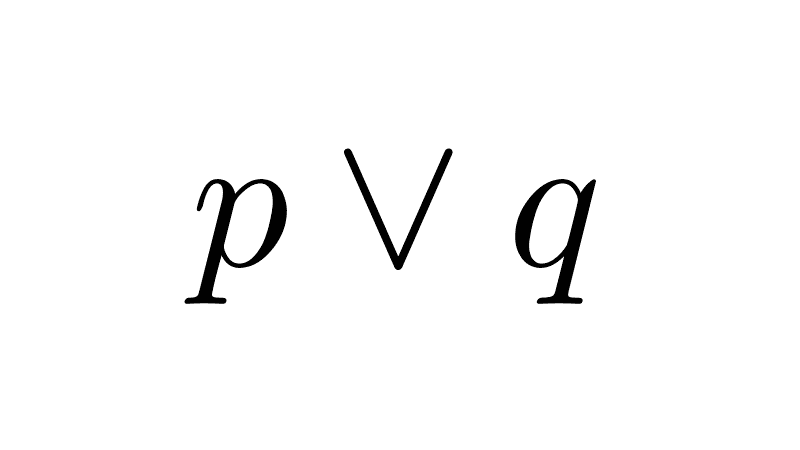
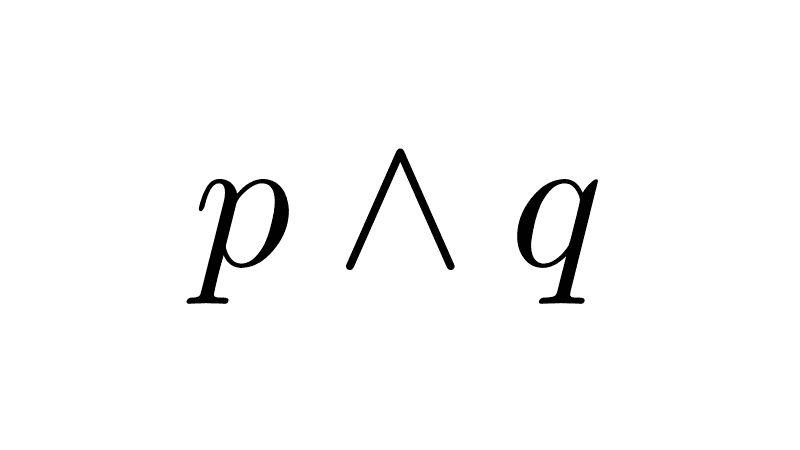
Otros artículos que te pueden interesar