Condicional lógico
El condicional lógico, también conocido como implicación, es un conectivo lógico que enlaza dos proposiciones para formar una nueva donde se expresa que si la primera es verdadera, entonces la segunda también debe serlo. Se simboliza formalmente como p → q y se lee "si p, entonces q”; en esta estructura, p recibe el nombre de antecedente (la condición), mientras que q es el consecuente (el resultado).
Lo que define al condicional es que solo es falso en un caso: cuando el antecedente es verdadero y el consecuente es falso; en todas las demás combinaciones de valores de verdad, la implicación se considera verdadera. Esta regla implica una particularidad importante: si el antecedente es falso, el condicional es verdadero sin importar el valor del consecuente. Aunque este comportamiento pueda parecer contraintuitivo en el lenguaje cotidiano, es fundamental para la coherencia de la lógica formal.
Veamos algunos ejemplos para aclarar cómo funciona en la práctica:
- "Si estudias, entonces apruebas": esta proposición solo sería falsa en un caso: si estudias (p verdadero) y no apruebas (q falso). Si no estudias, la promesa original no se incumple, sin importar si apruebas o no.
- "Si llueve, entonces la calle se moja": esta afirmación es falsa únicamente si está lloviendo y, aun así, la calle permanece seca. Si no llueve, la implicación se mantiene verdadera, independientemente de que la calle esté mojada por otra razón (como un camión de limpieza).
- "Si 2 + 2 = 5, entonces el cielo es azul": aunque no haya relación entre ambas ideas, desde el punto de vista lógico la implicación es verdadera, porque el antecedente es falso. La lógica no juzga el contenido, solo la combinación de valores de verdad.
Índice
Tabla de verdad
La regla fundamental del condicional es sencilla: p → q es falsa solamente cuando p es verdadera y q es falsa. En todos los demás casos, la implicación es verdadera. Este comportamiento queda claro al revisar su tabla de verdad:
| p | q | p → q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
Analicemos cada caso:
- Si p es verdadera y q es verdadera, la implicación se cumple (verdadera).
- Si p es verdadera pero q es falsa, la implicación no se cumple (falsa).
- Si p es falsa, no importa el valor de q: la implicación se considera verdadera por defecto.
Una forma útil de entender el condicional es interpretarlo como una promesa: la única forma de romperla es que el antecedente se cumpla y el consecuente no. Por ejemplo, si decimos "si apruebas el examen, te regalo un libro", la promesa solo se rompe si apruebas el examen pero no recibes el libro. Si no apruebas, la promesa sigue en pie sin ser incumplida, independientemente de que te regalen el libro o no.
Esta peculiaridad lógica explica por qué una afirmación como "si 2 + 2 = 5, entonces existe vida en Marte" se considera formalmente verdadera: al ser el antecedente falso, la "promesa" no se incumple, por lo que la implicación se sostiene independientemente de la veracidad del consecuente.
Existen diferentes formas de leer la expresión p → q, las más comunes son:
- Si p, entonces q.
- p implica q.
- p es suficiente para q.
- q es necesario para p.
Implicaciones asociadas
A partir de una implicación directa p → q, podemos definir tres variantes lógicas que nos ayudan a analizar la relación desde diferentes perspectivas:
1) Recíproca: q → p
Aquí intercambiamos antecedente y consecuente. Por ejemplo, si la proposición original es "si llueve, la calle se moja", la recíproca sería "si la calle está mojada, entonces llueve".
2) Contraria: ¬p → ¬q
En este caso negamos ambas proposiciones manteniendo el orden original. Con el ejemplo anterior, la contraria es "si no llueve, entonces la calle no se moja".
3) Contrarrecíproca: ¬q → ¬p
En este caso negamos ambas proposiciones y las intercambiamos. Con nuestro ejemplo sería “si la calle no está mojada, entonces no llueve".
Una de las propiedades más importantes del condicional es que toda implicación es lógicamente equivalente a su contrarrecíproca. Es decir:
p → q ≡ ¬q → ¬p
Esto se puede demostrar con una tabla de verdad viendo que ambas proposiciones compuestas tienen el mismo valor de verdad en cada interpretación posible.
| p | q | ¬p | ¬q | p → q | ¬q → ¬p | p → q ≡ ¬q → ¬p |
|---|---|---|---|---|---|---|
| V | V | F | F | V | V | V |
| V | F | F | V | F | F | V |
| F | V | V | F | V | V | V |
| F | F | V | V | V | V | V |
Es importante destacar que ni la recíproca ni la contraria son equivalentes a la implicación original. Volviendo a nuestro ejemplo:
- La recíproca "si la calle está mojada, entonces llueve" puede ser falsa (la calle podría estar mojada por otros motivos).
- La contraria "si no llueve, entonces la calle no se moja" también puede ser falsa (podrían haber regado la calle).
Propiedades
El condicional simple cumple con varias propiedades fundamentales que permiten manipular y simplificar expresiones en lógica proposicional. A continuación, presentamos las más relevantes:
1) Equivalencia como disyunción: una de las transformaciones más útiles es expresar la implicación como una disyunción es la siguiente:
p → q ≡ ¬p ∨ q
Esta equivalencia se utiliza frecuentemente para simplificar demostraciones y análisis lógicos. Podemos confirmar que es cierto usando la creando la tabla de verdad:
| p | q | ¬p | p → q | ¬p ∨ q | p → q ≡ ¬p ∨ q |
|---|---|---|---|---|---|
| V | V | F | V | V | V |
| V | F | F | F | F | V |
| F | V | V | V | V | V |
| F | F | V | V | V | V |
2) Negación de una implicación: para negar un condicional, aplicamos la siguiente equivalencia:
¬(p → q) ≡ p ∧ ¬q
Esto confirma que la única forma de falsear "si p entonces q" es cuando p es verdadero y q es falso.
3) Contrarrecíproco: como mencionamos anteriormente, toda implicación es equivalente a su contrarrecíproco:
p → q ≡ ¬q → ¬p
Esta propiedad es fundamental en demostraciones matemáticas indirectas.
4) Transitividad (silogismo hipotético): si una condición implica una segunda, y esta a su vez implica una tercera, entonces la primera implica la tercera:
[ (p → q) ∧ (q → r) ] → (p → r)
5) Modus Ponens: esta es una regla de inferencia que nos permite afirmar el consecuente cuando el antecedente se cumple:
[ (p → q) ∧ p ] → q
6) Modus Tollens: si una implicación es verdadera pero su consecuente es falso, entonces el antecedente también debe ser falso:
[ (p → q) ∧ ¬q ] → ¬p
6) Exportación-Importación: esta regla nos permite reescribir implicaciones consecutivas como una sola expresión:
(p ∧ q → r) ≡ (p → (q → r))
7) Reducción al absurdo: si al suponer p obtenemos tanto q como ¬q, entonces p debe ser falso:
(p → q) ∧ (p → ¬q) ≡ ¬p
Esta técnica es ampliamente utilizada en demostración de teoremas.
8) Relación con tautologías y contradicciones: sea V una tautología (una proposición siempre verdadera) y F una contradicción (una proposición siempre falsa), entonces:
p → V ≡ V
p → F ≡ ¬p
V → p ≡ p
F → p ≡ V
A diferencia de otros conectivos, la implicación no cumple ciertas propiedades:
- No es conmutativa: p → q no es equivalente a q → p.
- No es idempotente: p → p ≡ V, pero no se reduce a p.
- No es asociativa en el sentido tradicional como otros operadores.
Condicionales en teoremas matemáticos
La estructura "si..., entonces..." es la base de la mayoría de los teoremas matemáticos, donde se establece una relación entre una hipótesis (condición inicial) y una tesis (conclusión que se deriva). Esta formulación garantiza que, siempre que se cumpla la hipótesis, necesariamente debe cumplirse la tesis.
Ejemplo: "si un número es divisible entre 4, entonces es par"
Analicemos diferentes casos:
1) Se cumple hipótesis y tesis:
Tomemos el número 8. Es divisible entre 4 (hipótesis verdadera) y efectivamente es par (tesis verdadera). El teorema se cumple.
2) Se cumple la hipótesis pero NO se cumple la tesis:
¿Existe algún número divisible entre 4 que no sea par? No, porque todo múltiplo de 4 es también múltiplo de 2. Este caso no existe, lo que confirma la validez del teorema.
3) NO se cumple hipótesis pero SÍ se cumple tesis:
Consideremos el número 6. No es divisible entre 4 (hipótesis falsa), pero sí es par (tesis verdadera). El teorema sigue siendo válido porque solo garantiza algo cuando la hipótesis se cumple. Dicho de otro modo, si la hipótesis no se cumple puede ocurrir cualquier cosa en la tesis y el teorema seguirá siendo válido.
4) NO se cumple hipótesis NI tesis:
El número 5 no es divisible entre 4 (hipótesis falsa) y tampoco es par (tesis falsa). El teorema permanece válido pues no exige nada cuando la hipótesis es falsa.
Es importante entender que el teorema "si un número es divisible entre 4, entonces es par" no afirma que todos los números pares sean divisibles entre 4 (eso sería la recíproca, que es falsa). Solo establece una dirección específica: la divisibilidad entre 4 como condición suficiente para ser par.
El uso del contrarecíproco resulta especialmente útil en la demostración de teoremas, ya que, como hemos visto, p → q ≡ ¬q → ¬p. Esto significa que, en lugar de probar directamente que “si se da la hipótesis, entonces se cumple la tesis”, podemos demostrar que “si no se cumple la tesis, entonces no se da la hipótesis”. Ambos enunciados son lógicamente equivalentes, por lo que probar uno equivale a probar el otro.
En el ejemplo anterior, el contrarecíproco del teorema “si un número es divisible entre 4, entonces es par” sería: “si un número no es par, entonces no es divisible entre 4”. Esta formulación suele ser más fácil de verificar: si un número es impar, claramente no puede ser divisible entre 4. Así, al probar el contrarecíproco, hemos demostrado también la validez del teorema original. Esta técnica se emplea con frecuencia cuando la demostración directa resulta más complicada o menos intuitiva.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

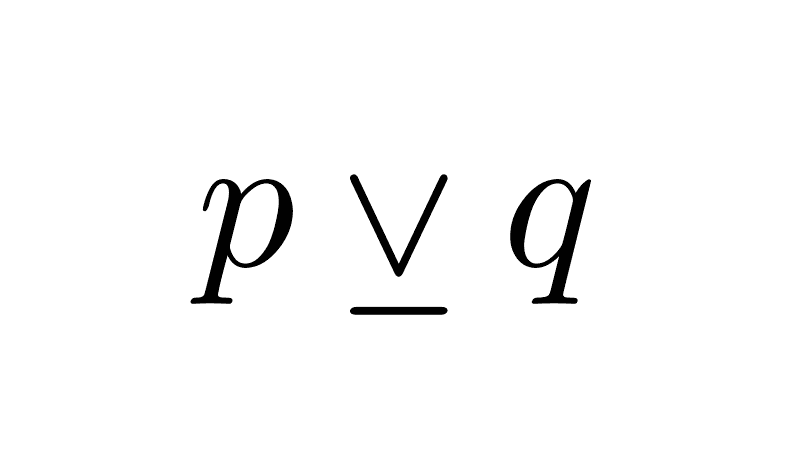
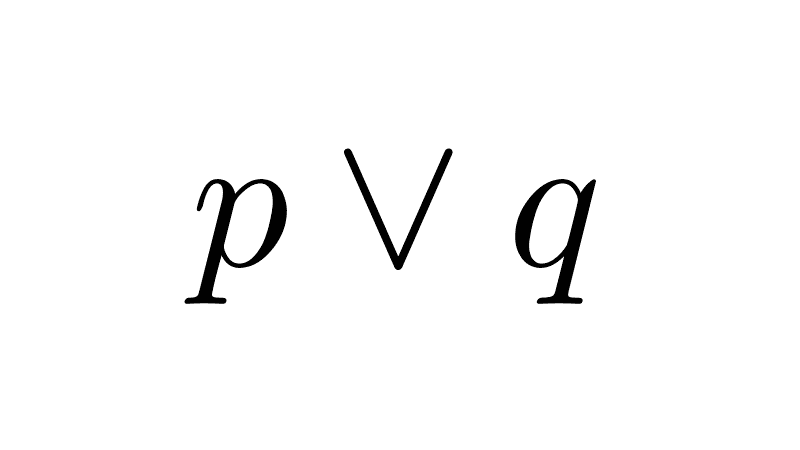
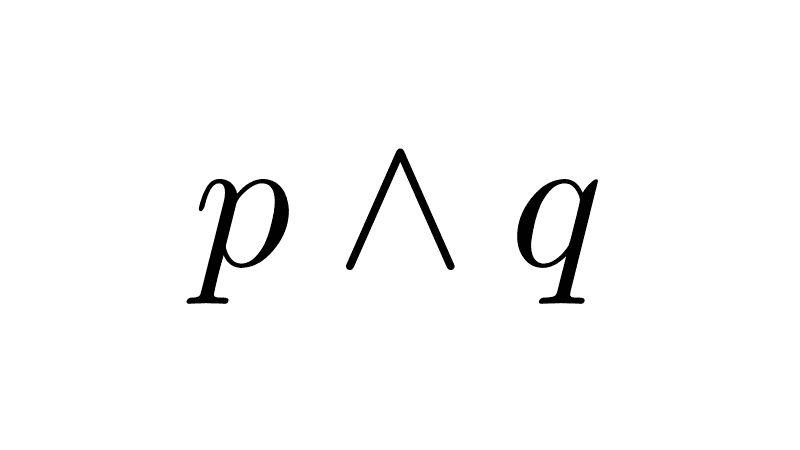
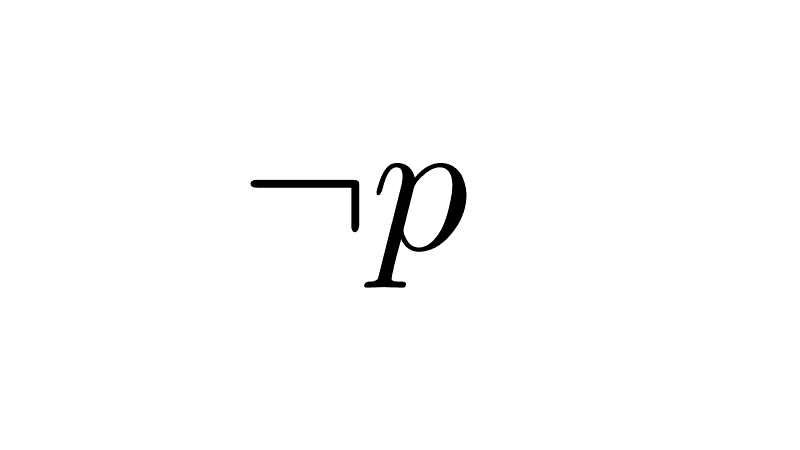
Otros artículos que te pueden interesar