Disyunción inclusiva
La disyunción, también conocida como disyunción inclusiva o débil, es un conectivo lógico que combina dos proposiciones simples para formar una proposición compuesta, la cual es verdadera cuando al menos una de las proposiciones simples es verdadera, y es falsa si ambas son falsas. La disyunción se representa con el símbolo ∨ y se lee como “o”.
Este conectivo representa el concepto cotidiano de "o" en su sentido más amplio e inclusivo. A diferencia del "o" excluyente que a veces usamos en el lenguaje común (como en "o vienes o te quedas"), la disyunción lógica ∨ no excluye la posibilidad de que ambas condiciones se cumplan simultáneamente.
Veamos algunos ejemplos para entender la disyunción inclusiva:
- "Para aprobar el curso, el estudiante debe entregar el proyecto final o presentar el examen sustitutorio”. En esta proposición vemos cómo actúa el “o” inclusivo, ya que si un estudiante solo entrega el proyecto, aprueba. Si solo presenta el examen, aprueba. Y, si hace ambas cosas, también aprueba.
- "Para entrar al evento, necesitas tener una invitación o ser socio del club". Cumplir con una sola condición (tener invitación o ser socio) es suficiente para entrar. Si una persona cumple ambas condiciones, también está habilitada.
- Si p es "hace calor" y q es "hay humedad", entonces p ∨ q significa "hace calor o hay humedad", entendiendo que esta afirmación es verdadera si ocurre uno u otro fenómeno, o ambos.
- Si p es "2 es un número par" (verdadero) y q es "2 es un número primo" (verdadero), entonces p ∨ q: "2 es un número par o es primo" es verdadera, ya que ambas proposiciones componentes lo son.
Una forma práctica de distinguirlo de otros conectivos es recordar que el símbolo ∨ se asemeja a una "V" (de "vel", la palabra latina para "o"), con el pico hacia abajo. No debe confundirse con el símbolo de la conjunción ∧ ("y"), que es un pico hacia arriba.
Existe otro tipo de disyunción llamada disyunción exclusiva, fuerte o diferencia simétrica. Su símbolo es ⊻ y se diferencia de la incluyente porque es verdadera sólo cuando una de las proposiciones que la conforman es verdadera, y es falsa si ambas son verdaderas o ambas falsas. En este artículo trataremos solamente el primer tipo de disyunción, la inclusiva.
Índice
Tabla de verdad
Como dijimos antes, la disyunción es verdadera cuando al menos una de las proposiciones que la componen es verdadera (o ambas lo son) y es falsa cuando ambas son falsas. Este comportamiento se visualiza mejor con una tabla de verdad:
| p | q | p ∨ q |
|---|---|---|
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
Por ejemplo, la proposición compuesta “hace calor o hay humedad, o ambas” es verdadera cuando es cierto que hace calor, que hay humedad o ambas al mismo tiempo; es falsa cuando no es cierta ninguna de las partes. El enunciado “2 es un número par o es primo” es verdadero porque las dos proposiciones son ciertas: 2 es par y también es primo.
La expresión “un triángulo tiene tres lados o un cuadrado tiene siete” es verdadera porque los triángulos sí tienen tres lados, aunque los cuadrados no tienen siete. Como una de las componentes es verdadera, la disyunción es verdadera. En cambio, la proposición “2+2=5 o 2+2=9” es una disyunción falsa porque no es cierto que 2+2=5 ni tampoco que 2+2=9.
Propiedades
La disyunción inclusiva cumple con una serie de propiedades que son esenciales para la manipulación y simplificación de fórmulas proposicionales. Las vemos a continuación.
1) Conmutatividad: el orden de las proposiciones no afecta el valor de verdad de la disyunción.
p ∨ q ≡ q ∨ p
2) Asociatividad: la agrupación de las proposiciones no afecta el valor de verdad de la disyunción.
(p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
3) Idempotencia: disyuntar una proposición consigo misma no aporta nueva información, el resultado es lógicamente equivalente a la proposición original.
(p ∨ p) ≡ p
4) Distributividad: la disyunción se distribuye sobre la conjunción y viceversa.
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
5) Elemento identidad o neutro: al disyuntar cualquier proposición con una contradicción (una proposición siempre falsa, F), el resultado es equivalente a la proposición original. La falsedad no contribuye a la veracidad de la disyunción.
(p ∨ F) ≡ p
6) Elemento dominante o absorbente: al disyuntar cualquier proposición con una tautología (una proposición siempre verdadera, V), el resultado es siempre verdadero, independientemente del valor de p. La tautología "domina" la operación.
(p ∨ V) ≡ V
7) Complementación (ley del tercero excluido): al disyuntar una proposición con su negación, el resultado es una tautología (siempre verdadera).
(p ∨ ¬p) ≡ V
8) Negación de la disyunción (Ley de De Morgan): la negación de una disyunción es equivalente a la conjunción de las negaciones.
¬(p ∨ q) ≡ ¬p ∧ ¬q
9) Absorción: esta ley muestra cómo una disyunción puede ser "absorbida" o simplificada cuando una de sus componentes interactúa con una conjunción.
p ∨ (p ∧ q) ≡ p
10) Eliminación de la disyunción (silogismo disyuntivo): esta es una regla de inferencia que nos permite derivar una conclusión a partir de una disyunción y la negación de uno de sus componentes.
[(p ∨ q) ∧ ¬p] → q
[(p ∨ q) ∧ ¬q] → p
Disyunción en la teoría de conjuntos
En la teoría de conjuntos, la disyunción inclusiva encuentra su equivalente directo en la unión de conjuntos: una operación que combina dos o más conjuntos para formar uno nuevo que contiene todos los elementos que pertenecen a cualquiera de los conjuntos originales.
La unión de dos conjuntos A y B, denotada como A ∪ B, se define formalmente como:
A ∪ B = { x | x ∈ A ∨ x ∈ B }
Esta definición utiliza explícitamente el operador de disyunción inclusiva (∨). El elemento x pertenece a la unión si está en A, en B, o en ambos.
Veamos algunos ejemplos concretos de esta operación:
- Dados los conjuntos A = {1, 3, 5} y B = {2, 3, 4}, su unión es A ∪ B = {1, 2, 3, 4, 5}. Notamos que el elemento 3, que pertenece a ambos conjuntos, aparece una sola vez en el resultado, ya que un conjunto no admite elementos duplicados.
- Si definimos C como el conjunto de las vocales {a, e, i, o, u} y D como las primeras letras del alfabeto {a, b, c}, la unión C ∪ D resulta en {a, b, c, e, i, o, u}.
- Consideremos el conjunto de números pares positivos P = {2, 4, 6, ...} y el conjunto de números impares positivos I = {1, 3, 5, ...}. Su unión P ∪ I es igual al conjunto de todos los números naturales positivos, esto muestra que dos conjuntos disjuntos (sin elementos en común) pueden unirse para formar uno solo.
La unión de conjuntos, al igual que su contraparte lógica, cumple con una serie de propiedades fundamentales:
- Conmutatividad: A ∪ B = B ∪ A.
- Asociatividad: (A ∪ B) ∪ C = A ∪ (B ∪ C).
- Distributividad sobre la intersección: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
- Idempotencia: A ∪ A = A.
- Elemento identidad: A ∪ ∅ = A (∅ es el conjunto vacío).
- Elemento dominante: A ∪ U = U (U es el conjunto universal).
- Ley del complemento: A ∪ A' = U (A’ es el complemento de A).
Disyunción en un circuito lógico
En el ámbito de la electrónica digital y la arquitectura de computadoras, la disyunción inclusiva se materializa físicamente en un componente fundamental: la puerta lógica OR. Esta puerta recibe una o más señales de entrada (generalmente dos) y produce una sola salida.
Su funcionamiento se basa en un principio simple: la salida será 1 (verdadero o "alto") si al menos una de sus entradas es 1. Si todas las entradas son 0 (falso o "bajo"), la salida será 0. Este comportamiento se representa en una tabla de verdad:
| Entrada A | Entrada B | Salida (A OR B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
En la mayoría de los lenguajes, la disyunción inclusiva se representa con el operador || (como en C, Java, JavaScript). Por ejemplo, en una condición como if (llueve || haceFrio), el bloque de código se ejecutará si ocurre al menos uno de los dos eventos, o ambos. Algunos lenguajes, como Python o SQL, también utilizan la palabra OR.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

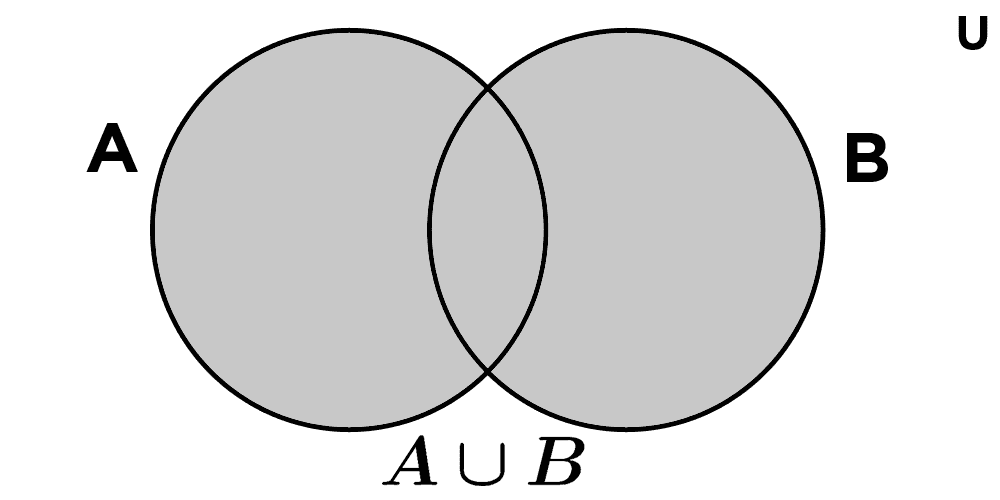
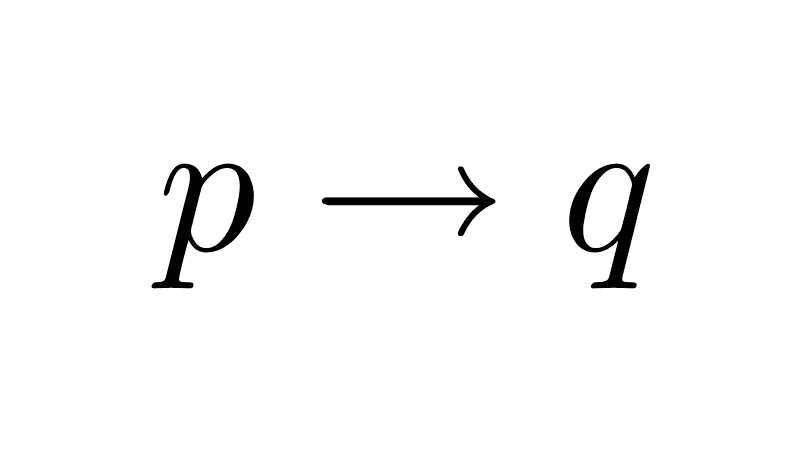
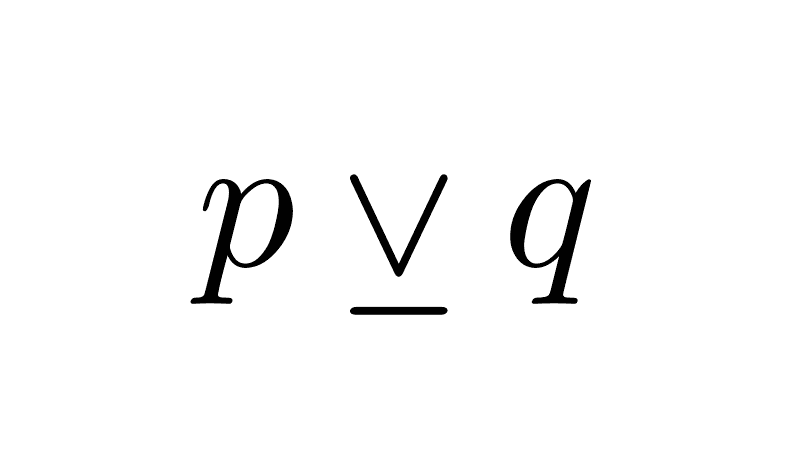
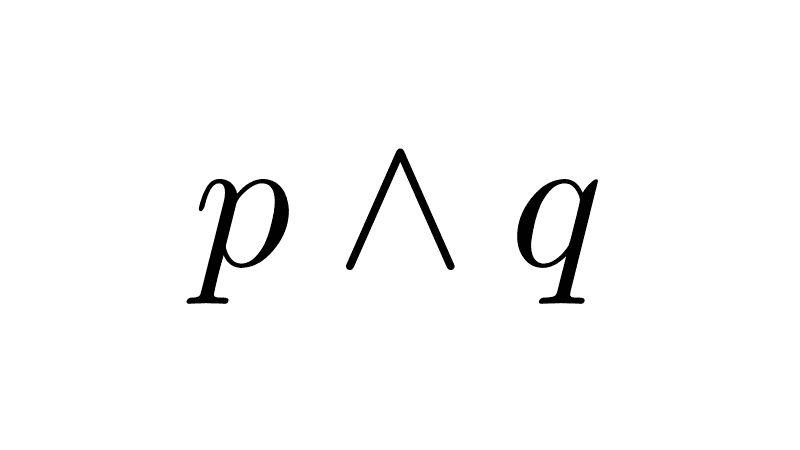
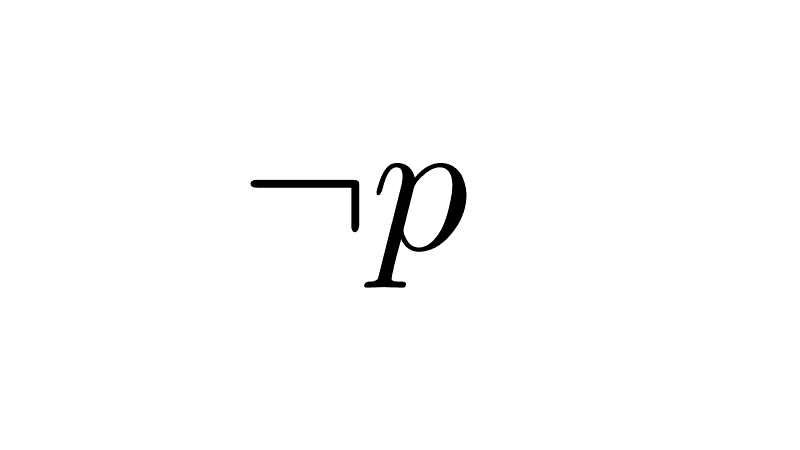
Otros artículos que te pueden interesar