Disyunción exclusiva
La disyunción exclusiva, también conocida como fuerte o excluyente, es un conectivo lógico que une dos proposiciones y devuelve un valor verdadero solo cuando una de ellas es verdadera, pero no ambas. Se representa con el símbolo ⊻ o ⊕ y se lee como "o… o…, pero no ambos".
A diferencia de la disyunción inclusiva (∨), que admite que ambas proposiciones sean verdaderas, la disyunción exclusiva excluye esa posibilidad. Es decir, es verdadera únicamente cuando las dos proposiciones tienen valores de verdad distintos.
Algunos ejemplos de disyunción exclusiva son:
- "La luz o está encendida o está apagada": una lámpara no puede estar encendida y apagada al mismo tiempo. Si una es verdadera, la otra es falsa automáticamente.
- "Ese animal o es un perro o es un gato": si el animal es un perro, no puede ser un gato, y viceversa. Ambas posibilidades no pueden darse a la vez para un mismo individuo.
- "La llave o está dentro del cajón o está fuera de él": la llave no puede estar en ambos lugares simultáneamente; debe encontrarse en uno solo de los dos estados.
- Si p: "9 es par" y q: "9 es primo", entonces p ⊻ q es "el número 9 es par o es primo, pero no ambos". Esta proposición es falsa porque p y q tienen el mismo valor de verdad, ambos falsos.
Índice
Tabla de verdad
Como dijimos antes, la disyunción fuerte o exclusiva es verdadera sólo cuando una de las dos proposiciones es verdadera, y es falsa cuando ambas son verdaderas o ambas son falsas. Este comportamiento se representa en la siguiente tabla de verdad:
| p | q | p ⊻ q |
|---|---|---|
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
Ejemplos que ilustran la tabla de verdad de la disyunción fuerte:
- "O 7 es impar o 7 es primo": ambas proposiciones son verdaderas (7 es impar y es primo), por lo que la disyunción exclusiva es falsa.
- "4 es par ⊻ 4 es primo": la primera proposición es verdadera (4 es par) y la segunda es falsa (4 no es primo), por lo que la disyunción exclusiva es verdadera.
- "9 es primo o 10 es positivo, pero no ambos": la primera proposición es falsa y la segunda es verdadera (9 no es primo, pero 10 sí es positivo), por tanto, la proposición compuesta es verdadera.
- "15 es par o 15 es primo, pero no ambos": ambas proposiciones son falsas (15 no es par ni es primo), por lo que la disyunción exclusiva es falsa.
Propiedades
La disyunción excluyente cumple una serie de propiedades que veremos a continuación.
1) Conmutatividad: el orden de las proposiciones no altera el resultado.
p ⊻ q ≡ q ⊻ p
2) Asociatividad: cuando hay más de dos proposiciones conectadas por una disyunción excluyente, el agrupamiento no altera el resultado.
(p ⊻ q) ⊻ r ≡ p ⊻ (q ⊻ r)
3) Distributividad con la conjunción: la disyunción exclusiva se distribuye sobre la conjunción.
p ∧ (q ⊻ r) ≡ (p ∧ q) ⊻ (p ∧ r)
4) Elemento neutro: una contradicción (una proposición siempre falsa, F) actúa como elemento neutro o identidad.
p ⊻ F ≡ p
5) Elemento inverso o auto-negación: cada proposición es su propio inverso.
p ⊻ p ≡ F
6) Relación con la negación: negar una de las entradas es equivalente a negar toda la expresión.
p ⊻ ¬q ≡ ¬(p ⊻ q)
¬p ⊻ q ≡ ¬(p ⊻ q)
7) Cancelación: si p ⊻ q ≡ p ⊻ r, entonces se puede "cancelar" p, concluyendo que q ≡ r.
8) Equivalencias con otros operadores: la disyunción fuerte se puede expresar usando los operadores básicos (∧, ∨, ¬) de varias formas:
p ⊻ q ≡ (p ∧ ¬q) ∨ (¬p ∧ q)
(Esta es la definición misma: "p y no q, o no p y q").
p ⊻ q ≡ (p ∨ q) ∧ ¬(p ∧ q)
("Uno o el otro, pero no ambos").
La disyunción exclusiva es la negación del bicondicional: mientras que p ↔ q es verdadera cuando p y q tienen el mismo valor de verdad, p ⊻ q es verdadera cuando tienen valores diferentes.
p ⊻ q ≡ ¬(p ↔ q)
Disyunción excluyente en conjuntos
En teoría de conjuntos, la disyunción exclusiva tiene su equivalente directo en la diferencia simétrica: una operación que combina dos conjuntos para formar uno nuevo que contiene los elementos que pertenecen a uno de los conjuntos, pero no a ambos.
La diferencia simétrica entre dos conjuntos A y B, denotada como A Δ B, se define formalmente como:
A Δ B = { x | x ∈ A ⊻ x ∈ B }
Un elemento x pertenece a la diferencia simétrica si está en A o en B, pero no en los dos a la vez.
Ejemplos
- Dados A = {1, 2, 3} y B = {2, 3, 4}, su diferencia simétrica es A Δ B = {1, 4}. Los elementos 2 y 3, que pertenecen a ambos conjuntos, se excluyen del resultado.
- Si C = {a, e, i} y D = {e, o, u}, entonces C Δ D = {a, i, o, u}. Solo la vocal "e" queda excluida por aparecer en ambos conjuntos.
Propiedades de la diferencia simétrica:
- Conmutatividad: A Δ B = B Δ A
- Asociatividad: (A Δ B) Δ C = A Δ (B Δ C)
- Intersección distributiva: A ∩ (B Δ C) = (A ∩ B) Δ (A ∩ C)
- Elemento neutro: A Δ ∅ = A (∅ es el conjunto vacío).
- Autoanulación: A Δ A = ∅
- Relación con unión e intersección: A Δ B = (A ∪ B) - (A ∩ B)
Disyunción excluyente en circuitos lógicos
En electrónica digital, la disyunción exclusiva se implementa físicamente mediante la puerta lógica XOR. Este componente recibe dos señales de entrada y produce una salida que sigue el mismo comportamiento que el operador ⊻.
La puerta XOR devuelve un valor 1 (verdadero) solo cuando sus entradas son diferentes, y 0 (falso) cuando ambas entradas son iguales. Esta característica la hace fundamental para operaciones donde es crucial detectar diferencias.
| Entrada A | Entrada B | Salida (A XOR B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
En programación, la disyunción exclusiva cuenta con representación directa en varios lenguajes a través del operador “^”. Este símbolo se utiliza de forma consistente en lenguajes como C, C++, Java y Python para realizar la operación XOR entre dos valores booleanos o bits. Por ejemplo, la expresión “a ^ b” devuelve verdadero únicamente cuando los valores de “a” y “b” son diferentes.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

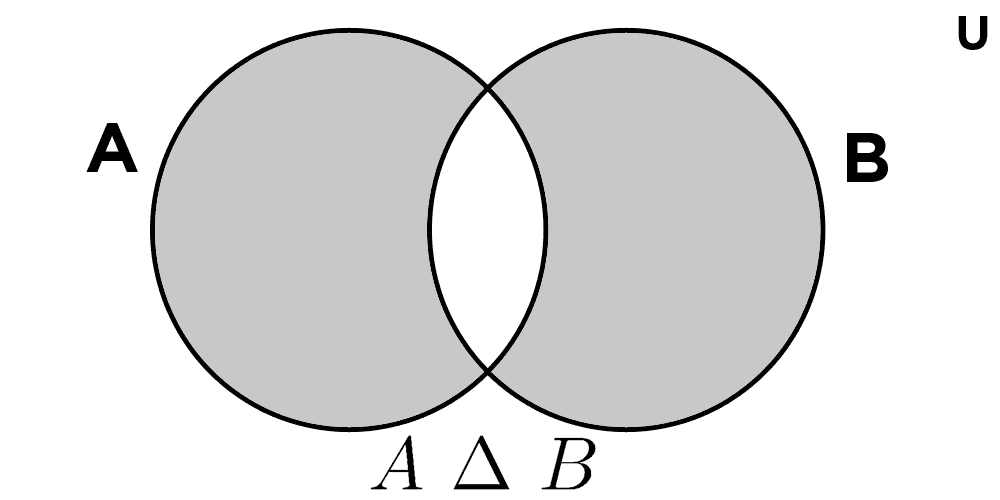
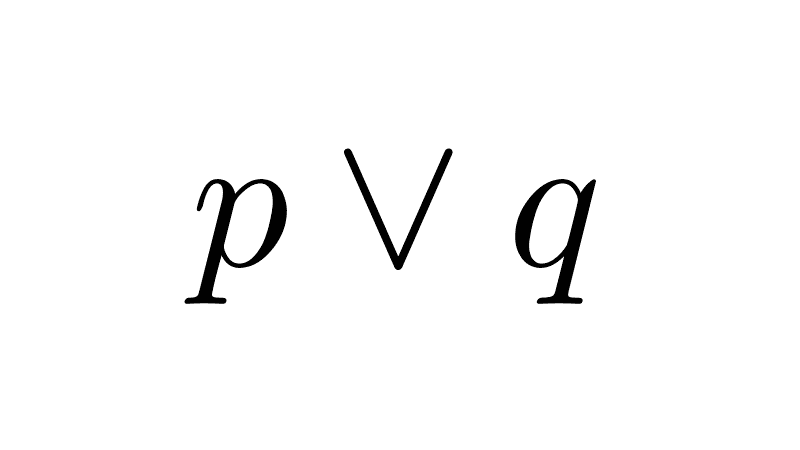
Otros artículos que te pueden interesar