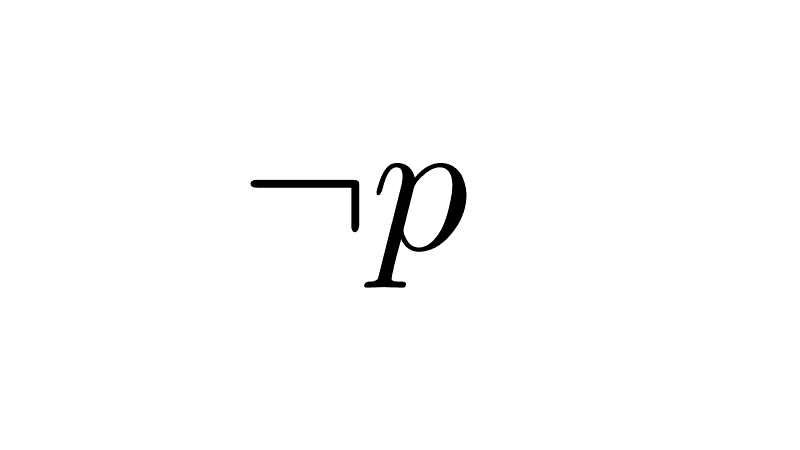
Conectivos lógicos en matemáticas
Los conectivos lógicos (también llamados conectores u operadores) son símbolos o palabras que permiten formar nuevas proposiciones a partir de otras ya existentes. En lógica proposicional, su función es unir dos o más proposiciones (simples o compuestas) para crear una proposición compuesta, cuyo valor de verdad dependerá de los valores de verdad de las proposiciones que la conforman.
Para entender mejor cómo funcionan, conviene recordar un concepto importante: una proposición es una oración declarativa que puede clasificarse de manera inequívoca como verdadera o falsa, pero nunca ambas a la vez. Ejemplos típicos son: "2 es un número par" (verdadera) o "5 es menor que 3" (falsa). En lógica, solemos representarlas con letras minúsculas como p, q, r, etc.
Así como en aritmética combinamos números mediante operaciones, en lógica combinamos proposiciones mediante conectores. La diferencia es que en lugar de obtener un número como resultado, obtenemos una proposición compuesta, cuyo valor de verdad se define a partir de las proposiciones iniciales.
En lógica proposicional, los conectivos lógicos más comunes son la negación (no), la conjunción (y), la disyunción (o), el condicional (si… entonces) y el bicondicional (si y sólo si). Para cada uno de ellos existen símbolos específicos y una forma clara de saber cuándo son verdaderos y cuándo son falsos.
Un aspecto fundamental es que las proposiciones compuestas pueden unirse nuevamente con otros conectores, lo que nos permite crear expresiones lógicas cada vez más complejas. Gracias a esto, los conectores lógicos se vuelven una parte crucial del razonamiento matemático, siendo esenciales para construir argumentos, llevar a cabo demostraciones y resolver problemas de manera rigurosa.
Índice
Tabla de los conectivos lógicos
| Símbolo | Conectivo lógico | Significado |
|---|---|---|
| ¬ (también ~) | Negación ¬p | no p no es cierto que p no ocurre que p es falso que p |
| ∧ | Conjunción p ∧ q | p y q p aunque q p pero q p sin embargo q p no obstante q p a pesar de q |
| ∨ | Disyunción p ∨ q | p o q o ambos o bien p o bien q |
| ⊻ | Disyunción exclusiva (o diferencia simétrica) p ⊻ q | p o q, pero no ambos o bien p o bien q, pero no ambos |
| → | Condicional (o implicación) p → q | sí p, entonces q solo si p entonces q p es suficiente para q q es necesario para p no p a menos que q |
| ↔ | Bicondicional (o doble implicación) p ↔ q | p si y solo si q p suficiente y necesario para q p es equivalente a q |
Negación
La negación de la proposición p es la proposición ¬p (se lee "no p"). El negador tiene el mismo significado que la partícula «no» del lenguaje ordinario. Al negar un enunciado, nuestra intención es decir que ese enunciado es falso. Si una proposición es verdadera, su negación es falsa; si una proposición es falsa, su negación es verdadera.
Representamos las condiciones de verdad de esta conectiva mediante una tabla. La columna inicial recoge los posibles valores de verdad de un determinado enunciado p. La columna siguiente indica los valores de verdad que corresponden a la negación del enunciado. Para el valor verdadero se usa la letra "V" y para el valor falso la letra "F"; en otros contextos puede utilizarse "1" para verdadero y "0" para falso.
| p | ¬p |
|---|---|
| V | F |
| F | V |
Ejemplo 1
p: "La Luna orbita a la Tierra"
¬p: "La Luna no orbita a la Tierra"
La proposición p es verdadera, porque la Luna sí orbita a la Tierra, por tanto la proposición ¬p es falsa.
Ejemplo 2
q: "Los peces pueden respirar fuera del agua"
¬q: "No es cierto que los peces pueden respirar fuera del agua"
La proposición q es falsa, lo que provoca que la proposición ¬q sea verdadera.
Ejemplo 3
r: "5 es un número par"
¬r: "5 es un número impar"
En este caso, la proposición original es falsa y su negación es verdadera.
Ejemplo 4
Si tenemos una proposición negada ¬p, podemos volver a negarla, generando la proposición ¬(¬p). Así, si comenzamos con:
p: "7 es un número primo"
La negamos para obtener:
¬p: "No es cierto que 7 es un número primo"
Y la volvemos a negar:
¬(¬p): "No es cierto que no es cierto que 7 es un número primo"
Debido a que al negar p una vez invertimos su valor de verdad, al negar la negación volvimos a invertirlo, regresando al estado inicial. Podemos comprobarlo mirando en la tabla de verdad:
| p | ¬p | ¬(¬p) |
|---|---|---|
| V | F | V |
| F | V | F |
Cuando dos proposciones tienen el mismo valor de verdad para cada posible interpretación, se dice que son equivalentes y se simboliza con "≡". Así, tenemos que ¬(¬p) ≡ p, esto se conoce como la ley de involución o negación de la negación. Existen otras leyes lógicas relacionadas con la negación que veremos más adelante.
Nota: la negación se conoce como un conector unitario, dado que niega una proposición y no la conecta con otra. En cambio, los otros operadores se llaman conectores binarios, ya que tienen un alcance doble: hacia la derecha y hacia la izquierda, es decir, afectan a dos variables.
Conjunción
La conjunción de las proposiciones p y q es la proposición p ʌ q (se lee "p y q"). El significado del conjuntor es idéntico al de «y» en lenguaje ordinario. Una conjunción es verdadera cuando sus componentes son verdaderos; es falsa en cualquier otro caso.
Representamos las condiciones de verdad mediante una tabla análoga a la anterior. En las primeras dos columnas se indican ordenadamente las cuatro combinaciones posibles de verdad y falsedad de las proposiciones p y q. La tercera columna indica los valores de verdad que corresponden a cada caso.
| p | q | p ∧ q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
Ejemplo 1
Sean las proposiciones p: "El piano es un instrumento musical" y q: "2 es un número par", entonces:
p ʌ q: "El piano es un instrumento musical y 2 es un número par"
La proposición p ʌ q es verdadera porque tanto p como q son proposiciones son verdaderas.
Ejemplo 2
Sean p: "El color del cielo es rojo" y q: "2 + 2 = 4", su conjunción es:
p ʌ q: "El cielo es rojo y 2+2 = 4"
La proposición compuesta p ʌ q es falsa porque, aunque q es verdadera, p es falsa.
Ejemplo 3
Definamos p: "8 es un número impar" y q: "8 es un número negativo", formamos la conjunción:
p ʌ q: "8 es un número impar y es negativo"
Como no es cierto que 8 sea impar y tampoco es cierto que 8 sea negativo, la conjunción p ʌ q es falsa.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
5,0 / 5 — 2 votos
Ejemplo 4
Sean p: "4 es un número par", q: "-2 es un número negativo" y r: "2,5 es un número entero".
p ʌ q: "4 es un número par y -2 es un número negativo"
p ʌ r: "4 es un número par y 2,5 es un número entero"
La proposición molecular p ʌ q es verdadera porque p y q son verdaderas. En cambio, p ʌ r es falsa porque r es falsa. También podemos formar una conjunción con más de dos proposiciones:
p ʌ q ʌ r: "4 es un número par, -2 es un número negativo y 2,5 es un número entero"
La proposición p ʌ q ʌ r es falsa porque, aunque p y q son verdaderas, r es falsa. Si cualquiera de las partes es falsa, la conjunción completa es falsa.
También podemos aplicar negaciones a las conjunciones, por ejemplo:
¬(p ʌ q): "No es cierto que «4 es un número par y -2 es un número negativo»"
Esta proposición es falsa, porque la conjunción original era verdadera. En cambio:
¬(p ʌ r): "Es falso que «4 es un número par y 2,5 es un número entero»"
La proposición es verdadera porque la conjunción original era falsa. La negación de una conjunción significa que no es cierto que ambas proposiciones son simultáneamente ciertas, es decir, alguna de ellas debe ser falsa (o ambas). En efecto: es falsa la parte en la que dice que 2,5 es entero. Aunque la parte donde afirma que 4 es par sea verdadera, lo que no es cierto es que las dos proposiciones son verdaderas.
Es importante aplicar paréntesis correctamente, ya que una proposición ¬(p ʌ q) no es lo mismo que ¬p ʌ q o que p ʌ ¬q. También, el orden en que aparecen las proposiciones en una conjunción no cambia el significado de la misma, es decir, la conjunción es conmutativa: p ʌ q ≡ q ʌ p. Esto se puede confirmar realizando la tabla de verdad correspondiente.
Disyunción incluyente (o inclusiva)
La disyunción de p y q es la proposición p ∨ q (se lee "p o q"). El disyuntor se puede considerar parcialmente como una traducción al lenguaje formal de la partícula del lenguaje ordinario «o». La disyunción de dos proposiciones es verdadera cuando al menos una de esas proposiciones es verdadera (y cuando ambas lo son); es falsa cuando ambas son falsas.
| p | q | p ∨ q |
|---|---|---|
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
Las condiciones de verdad de la disyunción son la "contraparte" de las condiciones de verdad de la conjunción. También, el símbolo de la disyunción (∨) es la imagen invertida del conjuntor (ʌ).
Para probar la verdad de una conjunción hace falta probar la de todos sus miembros; para probar la verdad de la disyunción, basta probar la de uno. Recíprocamente ocurre con la falsedad: la falsedad de una conjunción se establece con probar la de uno de sus miembros; mientras que la falsedad de la disyunción requiere probar la de todos.
Ejemplo 1
Sean p: "El Sol es un planeta" y q: "La Tierra es un planeta".
p ∨ q: "El Sol es un planeta o la Tierra es un planeta"
La proposición es verdadera porque q es verdadera.
Ejemplo 2
Definamos p: "Los peces pueden volar" y q: "3 es un número par", entonces:
p ∨ q: "Los peces pueden volar o 3 es un número par"
La proposición p ∨ q es falsa porque tanto p como q son falsas.
Ejemplo 3
Sean p: "4 es un número par", q: "-2 es un número negativo" y r: "2,5 es un número entero". Podemos formar:
p ∨ q: "4 es un número par o -2 es negativo"
La proposición p ∨ q es verdadera porque tanto p como q son verdaderas. También podemos construir:
p ∨ q ∨ r: "4 es un número par o -2 es negativo o 2,5 es un entero"
El enunciado anterior es verdadero porque al menos una de las proposiciones que la componen es verdadera (en este caso, p y q lo son), aunque la última sea falsa.
Del mismo modo que vimos antes, podemos aplicar negaciones a este conector, y también combinarlo con conjunciones u otros conectores que veremos más adelante. Por ejemplo:
¬(p ∨ q): "No es cierto que «4 es un número par o -2 es negativo»"
La proposición ¬(p ∨ q) es falsa debido a que p ∨ q es verdadera y la negación invierte su valor de verdad. La negación de una disyunción significa que no es cierto que alguna de las proposiciones que la componen es verdadera, sino que ambas deben ser falsas. Como puede verse en la tabla de verdad, en el único caso en que ¬(p ∨ q) es verdadera es cuando tanto p como q son falsas.
| p | q | p ∨ q | ¬(p ∨ q) |
|---|---|---|---|
| V | V | V | F |
| V | F | V | F |
| F | V | V | F |
| F | F | F | V |
La disyunción cumple la propiedad conmutativa, es decir, el orden de las proposiciones no altera el significado: p ∨ q ≡ q ∨ p.
Disyunción excluyente (o exclusiva)
La disyunción exclusiva de p y q es la proposición p ⊻ q (se lee "p o q, pero no ambos"). Es verdadera cuando solo una de las dos proposiciones es verdadera; es falsa si ambas son falsas o si ambas son verdaderas en simultáneo.
| p | q | p ⊻ q |
|---|---|---|
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
Este conectivo puede considerarse como la traducción al lenguaje formal de la partícula «o» en sentido excluyente, es decir, cuando se quiere indicar que ocurre una cosa o ocurre otra, pero no ambas a la vez. Se diferencia de la otra disyunción principalmente por eso.
Ejemplo 1
Sean p: "4 es un número par" y q: "6 es un número par"
p ⊻ q: "4 es un número par o 6 es un número par, pero no ambos"
La proposición p ⊻ q es falsa porque p y q son verdaderas simultáneamente.
Ejemplo 2
Sean p: "La Tierra es plana" y q: "La Tierra es esférica"
p ⊻ q: "La Tierra es plana o es esférica, pero no ambos"
En este caso, p ⊻ q es verdadera porque solo q es verdadera mientras que p es falsa.
Condicional (o implicación)
El condicional o implicación de las proposiciones p y q es la proposición p → q (se lee "si p entonces q" o "p implica q"). El implicador puede ser considerado como una formalización parcial de la partícula del lenguaje ordinario «si..., entonces...». La expresión que precede al símbolo se denomina antecedente (p), y la que sucede, consecuente o consiguiente (q).
Una implicación es verdadera cuando su antecedente es falso o cuando su consecuente es verdadero; es falsa cuando su antecedente es verdadero y su consecuente falso.
| p | q | p → q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
Ejemplo 1
Sean p: "Juan aprueba su examen" y q: "La madre de Juan le regalará un chocolate". Podemos formar:
p → q: "Si Juan aprueba su examen, entonces su madre le regalará un chocolate"
El conector condicional actúa como una promesa: la única forma de romper una promesa es que quien prometió algo no lo cumpla. En este ejemplo, la única manera de que no se cumpla la promesa es que Juan apruebe el examen pero su madre no le de el chocolate. En ese caso, p será verdadero y q falso, haciendo que p → q sea una proposición falsa.
En cualquier otro caso, la promesa se cumple:
- Juan aprueba el examen (p es V) y su madre le da el chocolate (q es V), entonces p → q es verdadera.
- Juan no aprueba su examen (p es F) y su madre aún así le da el chocolate (q es V), entonces p → q es verdadera.
- Juan no aprueba su examen (p es F) y su madre no le da el chocolate (q es F), hace que p → q sea verdadera.
Nota: se podría pensar que el segundo caso es incorrecto ya que Juan no aprueba pero aún así recibe el regalo. En realidad, la promesa inicial era que si aprobaba, recibiría el regalo, pero no nos dice nada acerca de qué pasa si no aprueba. Por tanto, si Juan no aprueba, su madre tiene libertad de decidir si darle o no el regalo ya que no está rompiendo la promesa inicial.
Ejemplo 2
Sean p: "Los gatos pueden volar" y q: "4 es un número par". Podemos formar la implicación
p → q: "Si los gatos pueden volar, entonces 4 es un número par"
La proposición p → q es verdadera porque el antecedente p es falso, entonces no importa cuál sea el valor de verdad del consecuente q, la implicación será verdadera de todos modos.
El ejemplo puede chocar con la idea que tenemos acerca de que en una implicación debe existir alguna relación entre el contenido del antecente y el consecuente. En este caso, los gatos no tienen nada que ver con los números pares, pero la lógica matemática no se ocupa del contenido de las proposiciones, sino que únicamente se enfoca en la posibilidad de ser verdaderas o falsas. En otros términos, el condicional matemático no debe interpretarse como una relación de causa y efecto.
Formulación de teoremas
El condicional es uno de los conectores más utilizados en la formulación de teoremas matemáticos. Su estructura típica es hipótesis → tesis, donde la hipótesis es la condición inicial y la tesis es la conclusión que debe cumplirse siempre que la hipótesis sea verdadera.
En este sentido, si la hipótesis se cumple, necesariamente la tesis debe cumplirse también; en cambio, si la hipótesis no se cumple, el teorema sigue siendo válido aunque la conclusión pueda ser verdadera o falsa.
Por ejemplo, consideremos el siguiente enunciado:
"Si un número es múltiplo de 4, entonces es par"
Aquí la hipótesis es "el número es múltiplo de 4" y la tesis es "el número es par". El teorema es correcto: siempre que un número sea múltiplo de 4, también será par. Ahora bien, si la hipótesis no se cumple, como en el caso del número 5 (que no es múltiplo de 4), el teorema no se invalida.
Pensemos en el caso del número 6, este número no es múltiplo de 4, sin embargo sí es par. En este caso el teorema sigue siendo válido porque la hipótesis no se cumplió. El teorema no dice que todo número par debe ser múltiplo de 4; solo establece que si un número es múltiplo de 4, entonces es par.
De este modo, el condicional refleja la lógica interna de los teoremas: garantiza la validez cuando la hipótesis se cumple, pero no exige nada cuando no lo hace.
Implicaciones asociadas
Dada la implicación directa p → q, estas son sus asociadas:
- q → p es la implicación recíproca, donde permutamos las proposiciones.
- ¬p → ¬q es la implicación contraria o inversa, donde negamos ambas proposiciones sin cambiar su orden.
- ¬q → ¬p es la implicación contrarrecíproca, donde permutamos y negamos ambas proposiciones.
Toda implicación es equivalente a su contrarrecíproca, esto es p → q ≡ ¬q → ¬p. Con el ejemplo del teorema p → q: "Si un número es múltiplo de 4, entonces es par." podemos formar:
Recíproca: q → p: "Si un número es par, entonces es múltiplo de 4". Esta proposición es falsa, un contraejemplo es 6, el cual es par pero no es múltiplo de 4.
Contraria: ¬p → ¬q: "Si un número no es múltiplo de 4, entonces no es par". Este enunciado también es falso porque, por ejempo, 10 no es múltiplo de 4 pero sí es par.
Contrarrecíproca: ¬q → ¬p: "Si un número no es par, entonces no es múltiplo de 4". Esta proposición es verdadera ya que ningún número que no sea par puede ser múltiplo de 4.
Un ejemplo de la vida real podemos hacerlo con las proposiciones p: "Llueve" y q: "El patio está mojado":
- p → q: "Si llueve, entonces el patio está mojado".
- q → p: "Si el patio está mojado, entonces llueve".
- ¬p → ¬q: "Si no llueve, entonces el patio no está mojado".
- ¬q → ¬p: "Si el patio no está mojado, entonces no llueve".
Las implicaciones recíproca y contraria no son equivalentes a la original, pues el patio podría estar mojado aun cuando no esté lloviendo (alguien puede mojarlo echando agua). En cambio, si el patio no está mojado, sí podemos asegurar que no está lloviendo.
Bicondicional (o doble implicación)
La doble implicación de las proposiciones p y q es la proposición p ↔ q (se lee "p si y sólo si q"). Este conectivo puede considerarse como la traducción al lenguaje formal de la partícula «cuando y solamente cuando» y también de «equivale». Se emplea en el establecimiento de definiciones de equivalencias y en la expresión de condiciones necesarias y suficientes.
Una doble implicación es verdadera cuando sus dos componentes tienen el mismo valor de verdad, esto es, cuando ambos son verdaderos o ambos son falsos; y es falsa en caso contrario, o sea, cuando alguno de ellos es verdadero y el otro falso.
| p | q | p ↔ q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | V |
El bicondicional es lógicamente equivalente a la conjunción de dos implicaciones:
p ↔ q ≡ (p → q) ʌ (q → p)
Ejemplo 1
Sean p: "Está lloviendo" y q: "La calle está mojada", podemos formar la proposición:
p ↔ q: "Está lloviendo si y solo si la calle está mojada"
Si es cierto que está lloviendo (p es V) y también es cierto que la calle está mojada (q es V), la proposición p ↔ q es verdadera. Si no está lloviendo (p es F) y la calle no está mojada (q es F), el enunciado p ↔ q también es verdadero. Ahora bien, si alguna de las dos proposiciones p o q es falsa, el bicondicional será falso, esto es, cuando esté lloviendo (p es V) y la calle no esté mojada (q es F) o cuando la calle esté mojada (q es V) sin que esté lloviendo (p es F).
Ejemplo 2
Sean p: "Un número es par" y q: "Un número es divisible por 2".
p ↔ q: "Un número es par si y solo si es divisible por dos"
Si un número es par, entonces es divisible por 2 (por definición); y si un número es divisible por 2, entonces es par. La relación funciona en ambos sentidos, por tanto la proposición p ↔ q es verdadera.
Ejemplo 3
Definamos p: "Un triángulo es equilátero" y q: "Los tres lados de un triángulo son iguales"
p ↔ q: "Un triángulo es equilátero si y sólo si sus tres lados son iguales"
Si un triángulo es equilátero, sus tres lados son iguales; y si los tres lados de un triángulo son iguales, entonces decimos que es equilátero. Como se cumple en ambos sentidos, el bicondicional p ↔ q es verdadero.
Ejemplo 4
Sean p: "La suma de dos números es par" y q: "Dos números son pares".
p ↔ q: "La suma de dos números es par si y solo si los dos números son pares"
Esta proposición es falsa porque, si bien es cierto que la suma de dos números pares siempre es un número par (por ejemplo 2+2=4), también la suma de dos números impares da como resultado un número par (como 3+1=4).
Los símbolos más comunes para el bicondicional son "↔" y "⇔". La expresión "si y solo si" es comúnmente abreviada como "sii". Por ejemplo: "Un triángulo es equilátero sii sus tres lados son iguales".
Jerarquía de los conectivos lógicos
Al usar los símbolos lógicos, se establece una jerarquía entre ellos (también llamada precedencia o prioridad) que indica qué operaciones se realizan primero, evitando así el uso excesivo de paréntesis. La convención para evaluar los operadores es la siguiente:
- Negación (¬).
- Conjunción (∧).
- Disyunción (∨).
- Condicional (→).
- Bicondicional (↔).
Los signos de agrupación (paréntesis, corchetes y llaves) pueden alterar la precedencia, y siempre se evalúan primero.
Ejemplos
- ¬p ∧ q se interpreta como (¬p) ∧ q.
- p ∧ q ∨ r se interpreta como (p ∧ q) ∨ r.
- ¬p ∧ q → r se interpreta como [(¬p) ∧ q ] → r.
- p ∧ q → r ∨ s se interpreta como (p ∧ q) → (r ∨ s).
- p ↔ ¬q ∨ r lo interpretamos como p ↔ (¬q ∨ r).
- ¬p → q ↔ r ∧ s → t debe entenderse como (¬p → q) ↔ [(r ∧ s) → t].
Nótese que la negación sólo afecta a la proposición inmediata, salvo que un paréntesis lo modifique, por ejemplo, ¬(p ∧ q).
Ejercicios para practicar
Ejercicio: dadas las proposiciones:
p: "El cielo está nublado".
q: "Un triángulo tiene tres lados".
r: "Está lloviendo".
s: "Suena el timbre".
t: "El perro ladra".
Formule las siguientes proposiciones compuestas:
- ¬p ∧ q
- s → ¬(t ∨ r)
- p ⊻ s → t
- q ↔ ¬t
- ¬(r ∧ s)
- t → s
- p → q ∧ r
Soluciones
- ¬p ∧ q: "El cielo no está nublado y un triángulo tiene tres lados".
- s → ¬(t ∨ r): "Si suena el timbre, entonces no es cierto que el perro ladra o está lloviendo".
- p ⊻ s → t: "Si el cielo está nublado o suena el timbre (pero no ambos), entonces el perro ladra".
- q ↔ ¬t: "Un triángulo tiene tres lados si y solo si el perro no ladra".
- ¬(r ∧ s): "Es falso que está lloviendo y suena el timbre".
- t → s: "Si el perro ladra, entonces suena el timbre".
- p → q ∧ r: "Si el cielo está nublado, entonces un triángulo tiene tres lados y está lloviendo".
Bibliografía
- Acevedo González, G. (2011). Lógica Matemática. Universidad Nacional Abierta y a Distancia (UNAD).
- Copi, I. y Cohen, C. (2013). Introducción a la Lógica (2da edición). Limusa.
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
- Garrido, M. (1974). Lógica simbólica (4ta edición). Tecnos.
- Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
- Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
- Puyau, H. y Roetti, J. (1976). Elementos de Lógica Matemática. Editorial Universitaria de Buenos Aires.
Más información sobre cada conectiva
¿Te ha servido este contenido? ¡Califícalo!
5,0 / 5 — 2 votos
CÓMO CITAR ESTE ARTÍCULO
Machado, D. (2025, 5 de septiembre). Conectivos lógicos en matemáticas. Flamath. https://es.flamath.com/conectores-logicos
-
utilizando los conceptivos lógicos y o entonces Y si solo Sí para las proposiciones Carmen estudia mucho Carmen destaca en sus estudios forma proposiciones compuestas
-
Hola Daniel, muchas gracias por tan detallado trabajo, te escribo desde Ecuador, soy estudiante de educación básica y dentro de una de las materias de mi carrera me enviaron a estudiar las proposiciones y tu trabajo ha sido de gran ayuda, sigue así, te felicito.
3 Comentarios
Deja una respuesta

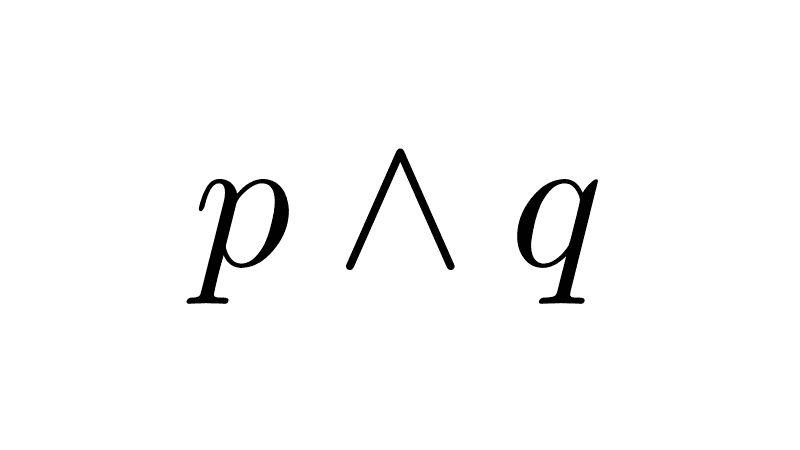
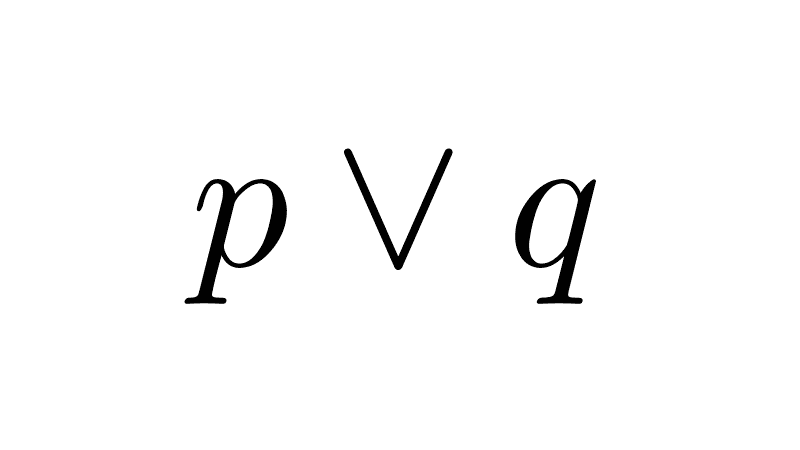
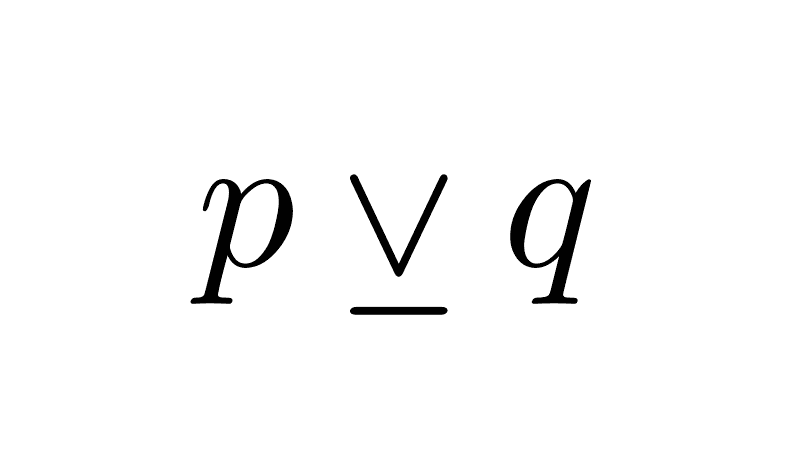
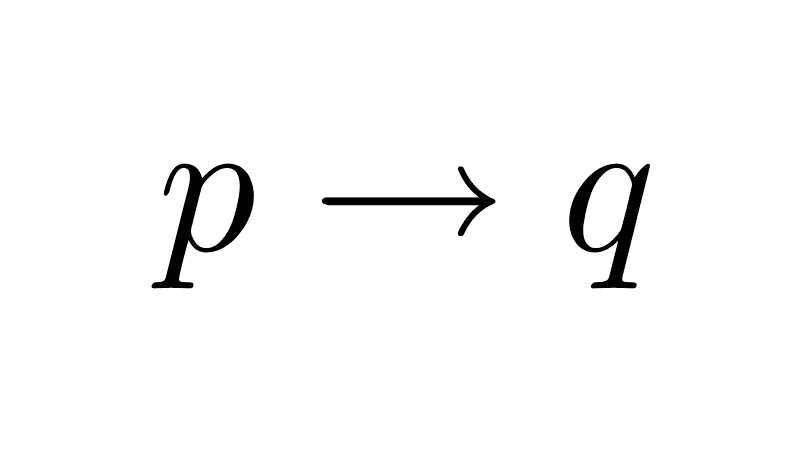
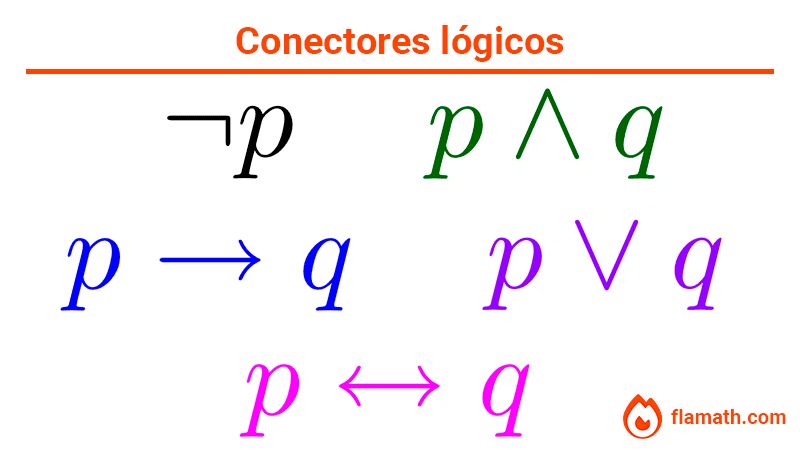





Otros artículos que te pueden interesar