Diferencia de conjuntos

La diferencia de conjuntos es una operación fundamental que produce un nuevo conjunto formado por los elementos que pertenecen a un primer conjunto, pero no a otro. Se representa mediante el símbolo menos "-".

La diferencia de conjuntos no es conmutativa. Esto significa que, en general, el orden de los conjuntos importa: A - B no es lo mismo que B - A. Mientras que la primera operación toma los elementos de A que no están en B, la segunda toma los de B que no están en A.

Otra forma de denominar a la diferencia entre A y B es como complemento relativo de B con respecto a A, simbolizado C_AB. También, una manera diferente de simbolizar a la diferencia A - B es usando una barra invertida en lugar del signo menos, así: A \ B.

Ejemplos

A continuación veremos algunos ejemplos de esta operación.

Ejemplo 1

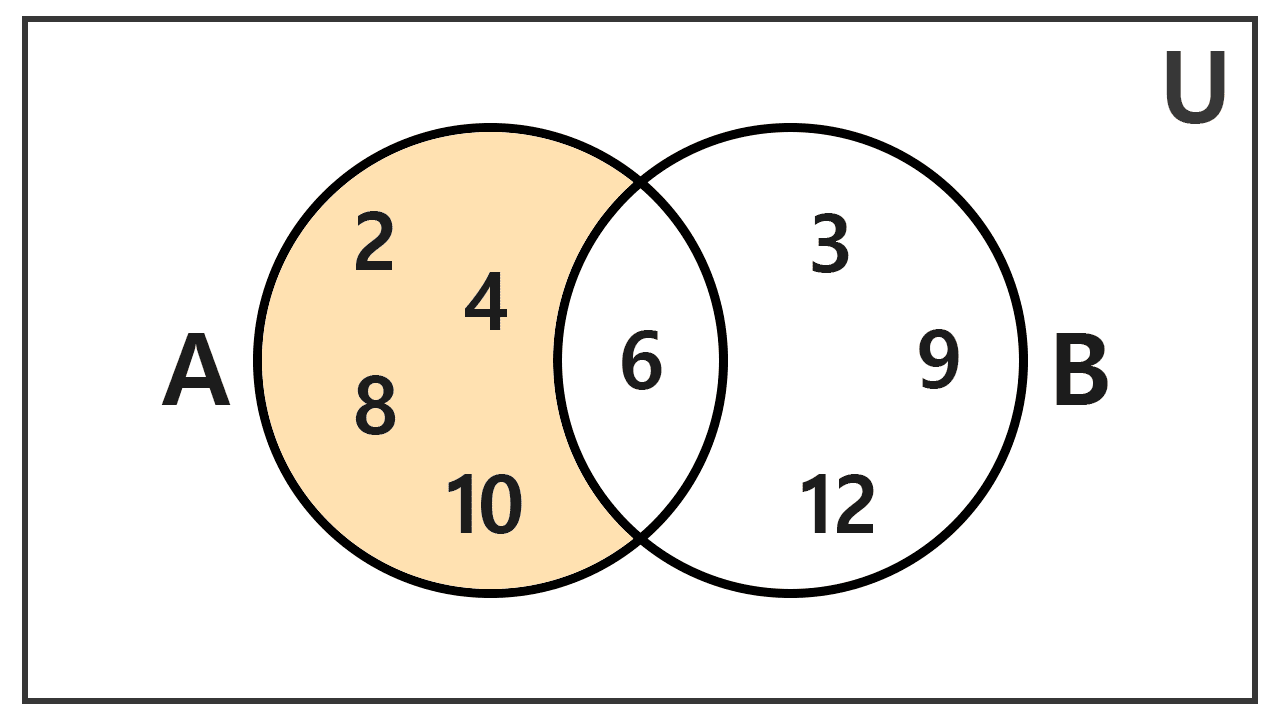
Sean los conjuntos A = {2, 4, 6, 8, 10} y B = {3, 6, 9, 12}. Calcular A - B y B - A.

Solución

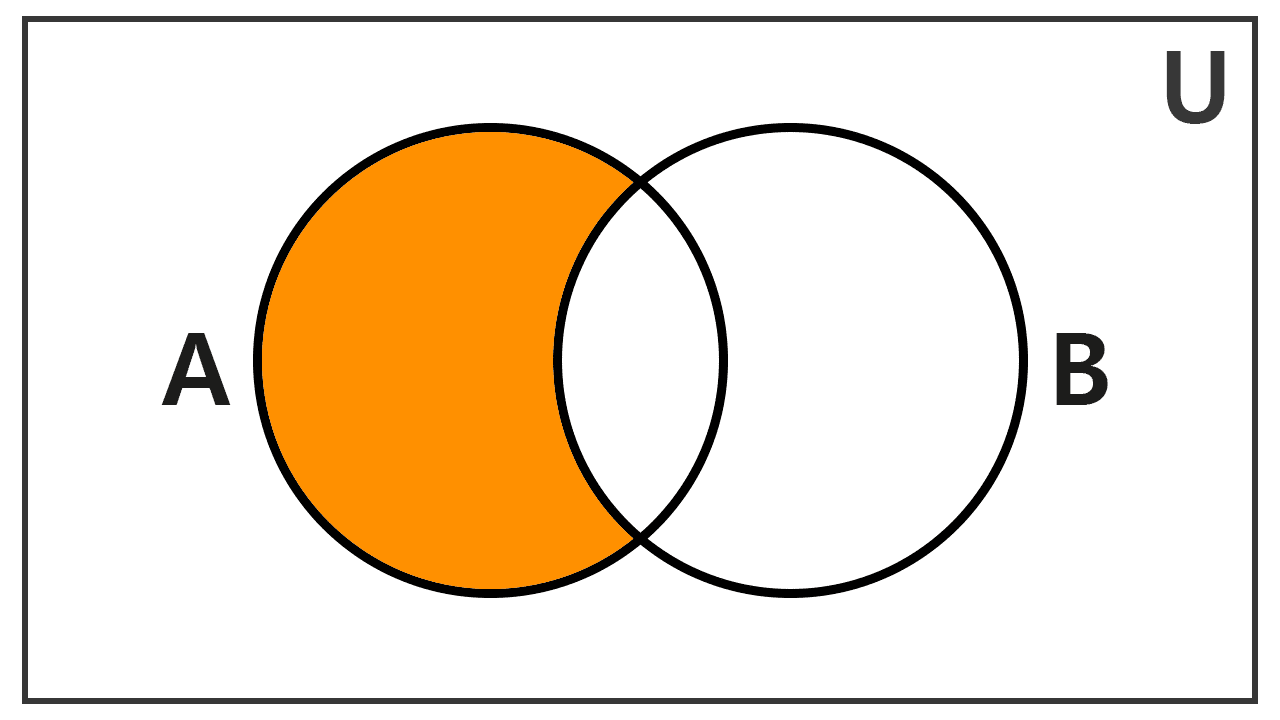
Para obtener A - B, tomamos los elementos de A y excluimos aquellos que también pertenecen a B. En A, los elementos son 2, 4, 6, 8 y 10. De estos, el 6 está presente en B, por lo que lo removemos. Así:

A - B = {2, 4, 8, 10}

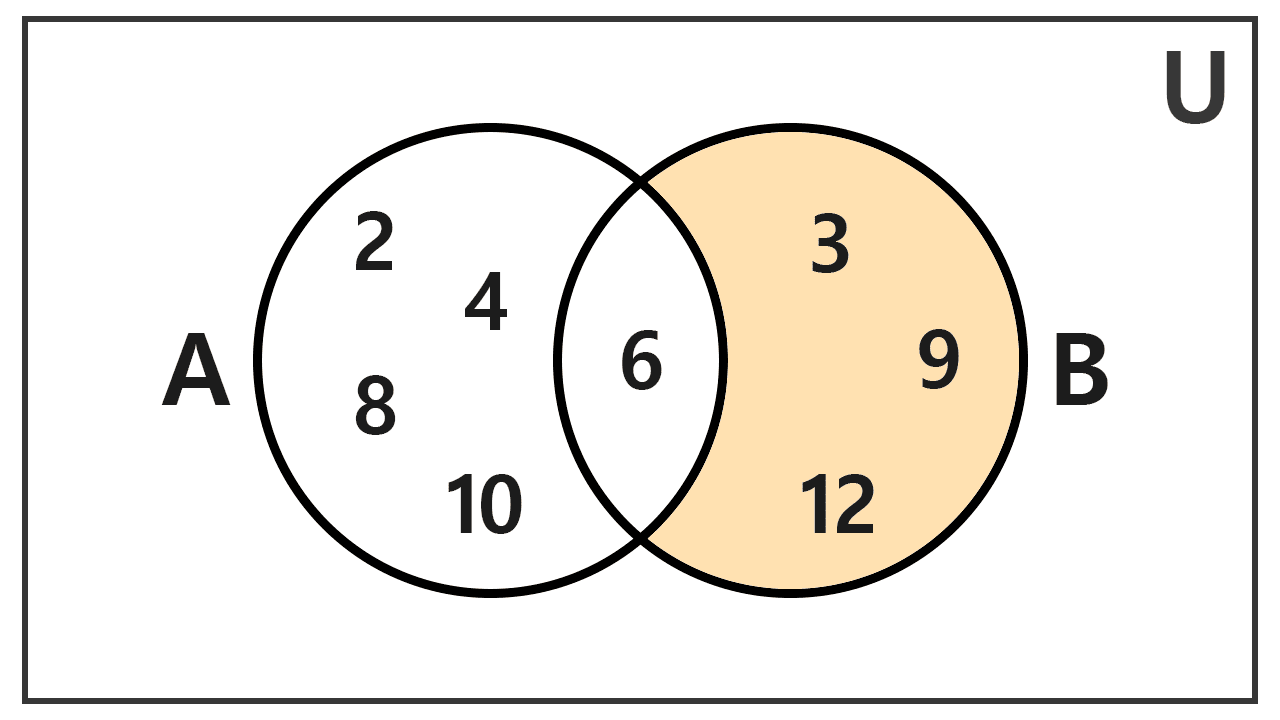
Para hallar B - A, consideramos los elementos de B y quitamos los que están en A. B contiene 3, 6, 9 y 12. El 6 aparece en A, así que lo eliminamos. El resultado es 

B - A = {3, 9, 12}

En este caso, ambas diferencias son conjuntos no vacíos y diferentes entre sí.

Ejemplo 2

Dados C = {a, e, i, o, u} y D = {a, b, c, d, e}, determinar C - D y D - C.

Solución

Calculamos primero C - D. Identificamos los elementos de C que no están en D: las vocales i, o y u no aparecen en D, por lo que:

C - D = {i, o, u}

Ahora, para D - C, tomamos los elementos de D y retiramos los que pertenecen a C. Las letras b, c y d de D no están en C, de modo que:

D - C = {b, c, d}

Ejemplo 3

Considerar E = {1, 3, 5, 7, 9} y F = {2, 4, 6, 8}. Hallar E - F y F - E.

Solución

E - F consiste en los elementos de E que no están en F. Como E y F no comparten ningún elemento, todos los elementos de E se conservan: 

E - F = {1, 3, 5, 7, 9} = E

Para F - E, todos los elementos de F se mantienen, ya que ninguno pertenece a E. Por tanto, 

F - E = {2, 4, 6, 8} = F

Aquí, aunque los conjuntos son disjuntos, E - F ≠ F - E, lo que refuerza la no conmutatividad de la operación.

Ejemplo 4

Sean G = {x, y, z} y H = {x, y, z}. Encontrar G - H y H - G.

Solución

G - H requiere los elementos de G que no están en H. Como G y H son iguales, no hay elementos en G que falten en H. Por lo tanto, G - H = ∅. De igual forma, H - G busca los elementos de H que no están en G. Al ser los conjuntos iguales, el resultado también es el conjunto vacío: H - G = ∅.

Ejemplo 5

Sea N el conjunto de los números naturales y P el conjunto de los números pares positivos, calcular N - P.

Solución

Escribimos algunos elementos de ambos conjuntos:

N = {1, 2, 3, 4, 5, 6, …}

P = {2, 4, 6, 8, 10, 12, …}

Si de N retiramos todos los elementos de P, nos queda el conjunto de los números impares I:

I = {1, 3, 5, 7, 9, 11, …}

Si quisiéramos calcular la diferencia P menos el conjunto N, obtendríamos el conjunto vacío, ya que todos los números pares positivos también son naturales.

Propiedades

La operación de diferencia en teoría de conjuntos posee un conjunto de propiedades y relaciones con otras operaciones.

1) No conmutatividad: el orden de los conjuntos en una diferencia sí altera el resultado.

A - B ≠ B - A

2) No asociatividad: la forma en que se agrupan los conjuntos afecta el resultado final.

(A - B) - C ≠ A - (B - C)

3) Elemento identidad (o neutro): la diferencia de cualquier conjunto con el conjunto vacío es el conjunto original. El conjunto vacío actúa como elemento neutro por la derecha.

A - ∅ = A

4) Diferencia con el conjunto universal: la diferencia de un conjunto con el conjunto universal es el conjunto vacío.

A - U = ∅

5) Relación con el complemento: la diferencia de conjuntos se utiliza para definir el complemento de un conjunto: el complemento de A es la diferencia del conjunto universal con A.

A' = U - A

6) Diferencia como intersección: la diferencia entre dos conjuntos es igual a la intersección del primero con el complemento del segundo.

A - B = A ∩ B'

Esto se demuestra por definición:

A - B = {x | x ∈ A ∧ x ∉ B} = { x | x ∈ A ∧ x ∈ B’ } = A ∩ B'

7) Diferencia de un conjunto consigo mismo: la diferencia de cualquier conjunto consigo mismo es siempre el conjunto vacío.

A - A = ∅

8) Conjuntos disjuntos: si dos conjuntos son disjuntos (no comparten elementos), entonces su diferencia es igual al primer conjunto. 

Si A y B son disjuntos (A ∩ B = ∅), entonces:

A - B = A

B - A = B

9) Propiedad de inclusión: si un conjunto es subconjunto de otro, su diferencia es el conjunto vacío.

Si A ⊆ B, entonces A - B = ∅

10) Distributividad de la intersección sobre la diferencia: la intersección es distributiva respecto a la diferencia.

A ∩ (B - C) = (A ∩ B) - (A ∩ C)

Para demostrar esta propiedad, partimos de la expresión del primer miembro y aplicamos la definición de diferencia como intersección con el complemento:

A ∩ (B - C) = A ∩ (B ∩ C') = (A ∩ B) ∩ C' (1)

Ahora consideramos el segundo miembro de la igualdad. Aplicamos nuevamente la definición de diferencia:

(A ∩ B) - (A ∩ C) = (A ∩ B) ∩ (A ∩ C)'

Utilizamos la Ley de De Morgan para transformar el complemento de una intersección:

= (A ∩ B) ∩ (A' ∪ C')

Aplicamos ahora la propiedad distributiva de la intersección respecto de la unión:

= [(A ∩ B) ∩ A'] ∪ [(A ∩ B) ∩ C']

Analizamos el primer término: (A ∩ B) ∩ A' = A ∩ B ∩ A'. Dado que A ∩ A' = ∅, tenemos: A ∩ B ∩ A' = ∅. Por lo tanto, la expresión se simplifica a:

= ∅ ∪ [(A ∩ B) ∩ C'] = (A ∩ B) ∩ C' (2)

Comparando los resultados (1) y (2), obtenemos:

A ∩ (B - C) = (A ∩ B) ∩ C' = (A ∩ B) - (A ∩ C)

Quedando así demostrada la igualdad.