
Leyes de De Morgan
Las leyes de De Morgan son dos reglas que nos permiten transformar y simplificar expresiones tanto en lógica proposicional como en la teoría de conjuntos. Estas leyes describen cómo se comporta la negación (en lógica) o el complemento (en conjuntos) cuando interactúa con los operadores principales.
En lógica proposicional, estas leyes nos permiten "distribuir" una negación que afecta a todo un paréntesis, transformando la negación de una conjunción en una disyunción de negaciones, y viceversa. En teoría de conjuntos, realizan la conversión análoga: transforman el complemento de una unión en una intersección de complementos, y el complemento de una intersección en una unión de complementos.
Estas leyes deben su nombre al matemático y lógico británico Augustus De Morgan (1806 - 1871), quien las formalizó en el siglo XIX, aunque se tenían indicios de su uso desde la Antigüedad.
Índice
Leyes en lógica proposicional
En lógica, las leyes de De Morgan nos permiten reescribir una negación que afecta a una proposición compuesta, lo cual resulta útil para simplificar proposiciones.
Fórmulas
Las dos reglas se expresan formalmente de la siguiente manera:
1) La negación de una conjunción es equivalente a la disyunción de las negaciones:
¬(p ∧ q) ≡ ¬p ∨ ¬q
2) La negación de una disyunción es equivalente a la conjunción de las negaciones:
¬(p ∨ q) ≡ ¬p ∧ ¬q
El símbolo "≡" significa que las expresiones a ambos lados son lógicamente equivalentes, siempre tienen el mismo valor de verdad.
La primera ley, ¬(p ∧ q) ≡ ¬p ∨ ¬q, nos dice esto: negar que dos cosas sucedan al mismo tiempo es equivalente a afirmar que al menos una de ellas no sucede.
Tomemos la frase: "Hoy es lunes y está lloviendo". Si alguien dice que esa afirmación es falsa, no está diciendo que "Hoy no es lunes y no está lloviendo", porque eso implicaría que ambas condiciones fallan. Lo que realmente significa es que no se dan ambas circunstancias juntas. En otras palabras: "Hoy no es lunes o no está lloviendo". Puede que no sea lunes, puede que no llueva, o pueden suceder ambas cosas. Lo único que descartamos es la combinación exacta de "lunes con lluvia".
De manera similar, la segunda ley, ¬(p ∨ q) ≡ ¬p ∧ ¬q, nos enseña cómo negar una elección o una posibilidad. Su mensaje es claro: negar que suceda una cosa o la otra es equivalente a afirmar que ninguna de las dos sucede.
Pensemos en la frase: "Voy al cine o al teatro". Si negamos esta declaración completa, diciendo "No es cierto que vaya al cine o al teatro", no estamos afirmando simplemente que no iremos a uno de los dos sitios, lo que estamos declarando es que no iremos a ninguno. Es decir, estamos afirmando con certeza: "No voy al cine y no voy al teatro".
Ejemplos de aplicación
Ejemplo 1
Consideremos las proposiciones simples:
p: "El café está caliente".
q: "El azúcar está disuelto".
La conjunción "El café está caliente y el azúcar está disuelto" se escribe como p ∧ q. Si afirmamos que esto no es cierto, escribimos ¬(p ∧ q). Aplicando la primera ley de De Morgan, esta negación equivale a ¬p ∨ ¬q, que se lee: "El café no está caliente o el azúcar no está disuelto".
Ejemplo 2
p: "El semáforo está en verde".
q: "El coche avanza".
La disyunción "El semáforo está en verde o el coche avanza" corresponde a p ∨ q. Su negación, ¬(p ∨ q), mediante la segunda ley se transforma en ¬p ∧ ¬q. Esto significa: "El semáforo no está en verde y el coche no avanza". Si no es cierto que al menos una de las acciones sucede, entonces ambas están ausentes.
Ejemplo 3
p: "El equipo gana el partido".
q: "Los jugadores celebran".
La conjunción p ∧ q sería "El equipo gana el partido y los jugadores celebran". Al negarla, ¬(p ∧ q), aplicamos la primera ley y obtenemos ¬p ∨ ¬q: "El equipo no gana el partido o los jugadores no celebran".
Esto refleja que para que la afirmación original sea falsa, no es necesario que fallen ambas circunstancias; basta con que el equipo pierda o que, aún ganando, no haya celebración.
Ejemplo 4
p: "La puerta está abierta".
q: "La luz está encendida".
La disyunción p ∨ q se enuncia como "La puerta está abierta o la luz está encendida". Su negación, según la segunda ley, es ¬p ∧ ¬q: "La puerta no está abierta y la luz no está encendida". Negar una opción entre dos implica que se descartan simultáneamente las dos posibilidades, una situación común cuando verificamos que un espacio está completamente cerrado y a oscuras.
Ejemplo 5
Consideremos las proposiciones matemáticas:
p: "El número 8 es par".
q: "El número 8 es primo".
La conjunción p ∧ q afirma: "8 es par y primo". Negar esta afirmación, ¬(p ∧ q), mediante la primera ley equivale a ¬p ∨ ¬q, lo que nos dice: "8 no es par o no es primo". Como 8 es par pero no es primo, la negación es verdadera porque se cumple la segunda parte de la disyunción ("8 no es primo").
Ejemplo 6
p: "El número -5 es positivo".
q: "El número -5 es compuesto".
La disyunción p ∨ q se lee: "-5 es positivo o es compuesto". Su negación, ¬(p ∨ q), se transforma con la segunda ley en ¬p ∧ ¬q. Esto significa: "-5 no es positivo ni es compuesto".
Dado que -5 no es positivo y tampoco es un número compuesto (es primo en valor absoluto, pero los números compuestos se definen para enteros positivos), ambas condiciones se cumplen, haciendo verdadera la negación de la disyunción original.
Ejemplo 7
Podemos emplear las leyes de De Morgan para simplificar expresiones lógicas.
Simplifiquemos la expresión ¬[ ¬(¬p ∨ q) ∨ ¬(p ∧ ¬q) ] paso a paso:
- ¬[ ¬(¬p ∨ q) ∨ ¬(p ∧ ¬q) ] (Expresión original).
- ¬[ (¬¬p ∧ ¬q) ∨ (¬p ∨ ¬¬q) ] (Aplicamos la segunda ley de De Morgan a ¬(¬p ∨ q) y la primera ley a ¬(p ∧ ¬q)).
- ¬[ (p ∧ ¬q) ∨ (¬p ∨ q) ] (Simplificamos las dobles negaciones: ¬¬p ≡ p y ¬¬q ≡ q).
- ¬(p ∧ ¬q) ∧ ¬(¬p ∨ q) (Aplicamos la segunda ley de De Morgan a la negación principal: ¬[A ∨ B] ≡ ¬A ∧ ¬B).
- (¬p ∨ ¬¬q) ∧ (¬¬p ∧ ¬q) (Aplicamos la primera ley a ¬(p ∧ ¬q) y la segunda ley a ¬(¬p ∨ q))
- (¬p ∨ q) ∧ (p ∧ ¬q) (Simplificamos las dobles negaciones nuevamente: ¬¬q ≡ q y ¬¬p ≡ p)
Una forma simplificada de la expresión original es (¬p ∨ q) ∧ (p ∧ ¬q). Esta fórmula se puede simplificar aún más pero nos detenemos aquí.
Existe una regla nemotécnica muy práctica para aplicar estas leyes: cuando una negación afecta a una expresión completa entre paréntesis (ya sea una conjunción o una disyunción), debemos "repartir" esa negación sobre cada uno de los elementos internos, cambiando simultáneamente el conector central por su opuesto (∨ se cambia por ∧ y viceversa).
Demostraciones de las leyes
La forma más directa de demostrar que dos expresiones lógicas son equivalentes es construyendo sus tablas de verdad y verificando que coinciden en todos los casos posibles. Vamos a hacerlo para la primera ley: ¬(p ∧ q) ≡ ¬p ∨ ¬q.
| p | q | ¬p | ¬q | p ∧ q | ¬(p ∧ q) | ¬p ∨ ¬q |
|---|---|---|---|---|---|---|
| V | V | F | F | V | F | F |
| V | F | F | V | F | V | V |
| F | V | V | F | F | V | V |
| F | F | V | V | F | V | V |
Como podemos observar, las columnas para ¬(p ∧ q) y ¬p ∨ ¬q son idénticas. Esto prueba que, sin importar los valores de verdad de p y q, ambas expresiones siempre dicen lo mismo.
Ahora, demostremos la segunda ley: ¬(p ∨ q) ≡ ¬p ∧ ¬q.
| p | q | ¬p | ¬q | p ∨ q | ¬(p ∨ q) | ¬p ∧ ¬q |
|---|---|---|---|---|---|---|
| V | V | F | F | V | F | F |
| V | F | F | V | V | F | F |
| F | V | V | F | V | F | F |
| F | F | V | V | F | V | V |
De nuevo, las columnas finales son idénticas, lo que demuestra la validez de la segunda ley.
Leyes en teoría de conjuntos
En teoría de conjuntos, los operadores de la lógica proposicional tienen sus equivalentes naturales: la disyunción (∨) corresponde a la unión (∪), la conjunción (∧) se traduce en la intersección (∩), y la negación (¬) se asocia al complemento de un conjunto, denotado como A'.
Esta correspondencia permite trasladar las leyes de De Morgan directamente al ámbito de los conjuntos, donde nos resultan igualmente útiles para transformar y simplificar expresiones que involucran complementos, uniones e intersecciones.
Fórmulas
Las dos reglas en teoría de conjuntos se expresan formalmente así:
1) El complemento de la unión de dos conjuntos es igual a la intersección de sus complementos:
(A ∪ B)' = A' ∩ B'
2) El complemento de la intersección de dos conjuntos es igual a la unión de sus complementos:
(A ∩ B)' = A' ∪ B'
En esencia, la primera ley nos dice que todo elemento que no pertenece a la unión de A y B (es decir, no está en ninguno de los dos), debe necesariamente estar fuera de A y fuera de B a la vez. La segunda ley afirma que todo elemento que no está en la intersección de A y B (no es común a ambos) o bien no está en A, o bien no está en B, o bien no está en ninguno.
Diagramas de Venn
Las leyes de De Morgan pueden visualizarse de manera muy intuitiva mediante los diagramas de Venn, donde las regiones sombreadas en anaranjado representan los conjuntos resultantes de las operaciones. A continuación, veremos las representaciones gráficas de ambas leyes.
Ejemplos
Veamos algunos ejemplos de aplicación de las leyes.
Ejemplo 1
Imaginemos que, en un centro de estudios, tenemos el conjunto L de personas inscritas en el curso de Lógica y el conjunto A de personas inscritas en el curso de Álgebra. La unión L ∪ A representa a todos los estudiantes que están inscritos en al menos uno de los dos cursos.
Si queremos describir al grupo de personas que no están inscritas en ningún curso, estamos hablando del complemento de la unión: (L ∪ A)'. Según la primera ley de De Morgan para conjuntos, este grupo es exactamente igual a la intersección de los complementos: L' ∩ A'. Es decir, son las personas que no están en el curso de Lógica y que no están en el curso de Álgebra. Si alguien falta en esta intersección, significa que está inscrito en al menos uno de los cursos.
Ejemplo 2
Consideremos ahora la intersección L ∩ A, que son los estudiantes inscritos simultáneamente en Lógica y Álgebra. Su complemento, (L ∩ A)', representa a todas las personas que no cursan ambas materias a la vez.
Aplicando la segunda ley, (L ∩ A)' = L' ∪ A'. Esto significa que una persona pertenece a este complemento si no está en el curso de Lógica, o no está en el curso de Álgebra, o no está en ninguno. Basta con que falte a uno de los dos cursos para que no pertenezca a la intersección original.
Ejemplo 3
Supongamos que en una biblioteca R es el conjunto de libros de romance y M el conjunto de libros de misterio. El bibliotecario necesita hacer una lista de los libros que no son ni de romance ni de misterio. Esta lista corresponde a (R ∪ M)'. Usando la ley, sabemos que estos libros son los que no son de romance (R') y, al mismo tiempo, no son de misterio (M'), es decir, son del conjunto R' ∩ M'.
Ejemplo 4
En un club deportivo, sea F el conjunto de miembros que juegan fútbol y T los que juegan tenis. El conjunto de miembros que no practican ambos deportes es (F ∩ T)'. Según la ley, esto equivale a F' ∪ T'. Por lo tanto, un miembro pertenece a este grupo si no juega fútbol, o no juega tenis. Incluso un miembro que solo juega uno de los dos deportes ya forma parte de este conjunto, pues no cumple con la condición de jugar los dos.
Ejemplo 5
Consideremos dos conjuntos de números A = {1, 2, 3, 4, 5} y B = {4, 5, 6, 7, 8}. Tomemos como universo el conjunto U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
La unión de A y B es A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8}. Su complemento (A ∪ B)' son los elementos de U que no están en esa unión, es decir, (A ∪ B)' = {9, 10}.
Apliquemos la primera ley de De Morgan: (A ∪ B)' debe ser igual a A' ∩ B'. Calculamos:
A' = {6, 7, 8, 9, 10} (números de U que no están en A).
B' = {1, 2, 3, 9, 10} (números de U que no están en B).
La intersección de estos complementos es A' ∩ B' = {9, 10}. Efectivamente, obtenemos el mismo resultado, confirmando que los únicos números en nuestro universo que quedan fuera de ambas "zonas" A y B son el 9 y el 10.
Ejemplo 6
Trabajemos ahora con conjuntos de letras. Definamos: C = {a, b, c, d, e} y D = {d, e, f, g, h}. Nuestro conjunto universal estará compuesto por las letras del alfabeto español hasta la "j":
U = {a, b, c, d, e, f, g, h, i, j}.
La intersección de C y D es C ∩ D = {d, e}. Su complemento (C ∩ D)' son todas las letras del universo que no son "d" ni "e". Es decir, (C ∩ D)' = {a, b, c, f, g, h, i, j}.
Verifiquemos la segunda ley: (C ∩ D)' debe ser igual a C' ∪ D'. Calculamos:
C' = {f, g, h, i, j} (letras de U que no están en C).
D' = {a, b, c, i, j} (letras de U que no están en D).
La unión de estos complementos es C' ∪ D' = {a, b, c, f, g, h, i, j}. Como vemos, el resultado coincide, las letras que no pertenecen a la intersección son aquellas que o bien están fuera de C, o bien fuera de D, o ambas.
Demostraciones
Podemos demostrar las leyes de De Morgan utilizando la definición de pertenencia a un conjunto y las propiedades de los conectivos lógicos. Vamos a probar la igualdad de conjuntos mostrando que un elemento pertenece a uno si y sólo si pertenece al otro.
1) Demostración de la primera ley: (A ∪ B)' = A' ∩ B'
Demostraremos que (A ∪ B)' ⊆ A' ∩ B' y que A' ∩ B' ⊆ (A ∪ B)'.
Parte 1: (A ∪ B)' ⊆ A' ∩ B'
Tomemos un elemento arbitrario x.
x ∈ (A ∪ B)' (Hipótesis)
⇒ x ∉ (A ∪ B) (Por definición de complemento)
⇒ ¬(x ∈ A ∨ x ∈ B) (Por definición de unión)
⇒ ¬(x ∈ A) ∧ ¬(x ∈ B) (Aplicando la ley de De Morgan de lógica)
⇒ x ∉ A ∧ x ∉ B (Por definición de negación de pertenencia)
⇒ x ∈ A' ∧ x ∈ B' (Por definición de complemento)
⇒ x ∈ (A' ∩ B') (Por definición de intersección)
Por lo tanto, si x ∈ (A ∪ B)', entonces x ∈ (A' ∩ B'). Esto prueba que (A ∪ B)' ⊆ A' ∩ B'.
Parte 2: A' ∩ B' ⊆ (A ∪ B)'
x ∈ (A' ∩ B') (Hipótesis)
⇒ x ∈ A' ∧ x ∈ B' (Por definición de intersección)
⇒ x ∉ A ∧ x ∉ B (Por definición de complemento)
⇒ ¬(x ∈ A) ∧ ¬(x ∈ B) (Por definición de negación de pertenencia)
⇒ ¬(x ∈ A ∨ x ∈ B) (Aplicando la ley de De Morgan de lógica)
⇒ x ∉ (A ∪ B) (Por definición de unión)
⇒ x ∈ (A ∪ B)' (Por definición de complemento)
Por lo tanto, si x ∈ (A' ∩ B'), entonces x ∈ (A ∪ B)'. Esto prueba que A' ∩ B' ⊆ (A ∪ B)'.
Como (A ∪ B)' ⊆ A' ∩ B' y A' ∩ B' ⊆ (A ∪ B)', concluimos que (A ∪ B)' = A' ∩ B'.
2) Demostración de la segunda ley: (A ∩ B)' = A' ∪ B'
Procedemos de manera análoga, demostrando la doble inclusión.
Parte 1: (A ∩ B)' ⊆ A' ∪ B'
Tomemos un elemento arbitrario x.
x ∈ (A ∩ B)' (Hipótesis)
⇒ x ∉ (A ∩ B) (Por definición de complemento)
⇒ ¬(x ∈ A ∧ x ∈ B) (Por definición de intersección)
⇒ ¬(x ∈ A) ∨ ¬(x ∈ B) (Aplicando la ley de De Morgan de lógica)
⇒ x ∉ A ∨ x ∉ B (Por definición de negación de pertenencia)
⇒ x ∈ A' ∨ x ∈ B' (Por definición de complemento)
⇒ x ∈ (A' ∪ B') (Por definición de unión)
Por lo tanto, (A ∩ B)' ⊆ A' ∪ B'.
Parte 2: A' ∪ B' ⊆ (A ∩ B)'
x ∈ (A' ∪ B') (Hipótesis)
⇒ x ∈ A' ∨ x ∈ B' (Por definición de unión)
⇒ x ∉ A ∨ x ∉ B (Por definición de complemento)
⇒ ¬(x ∈ A) ∨ ¬(x ∈ B) (Por definición de negación de pertenencia)
⇒ ¬(x ∈ A ∧ x ∈ B) (Aplicando la ley de De Morgan de lógica)
⇒ x ∉ (A ∩ B) (Por definición de intersección)
⇒ x ∈ (A ∩ B)' (Por definición de complemento)
Por lo tanto, A' ∪ B' ⊆ (A ∩ B)'.
Como (A ∩ B)' ⊆ A' ∪ B' y A' ∪ B' ⊆ (A ∩ B)', concluimos que (A ∩ B)' = A' ∪ B'.
Bibliografías consultadas
- Acevedo González, G. (2011). Lógica Matemática. Universidad Nacional Abierta y a Distancia (UNAD).
- Castillo P, E. y Pinta, M. (2015). Lógica Matemática I: Proposiciones y Leyes de Inferencia (2da edición). Universidad Técnica de Machala.
- Copi, I. y Cohen, C. (2013). Introducción a la Lógica (2da edición). Limusa.
- Garrido, M. (1974). Lógica simbólica (4ta edición). Tecnos.
- Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
- Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

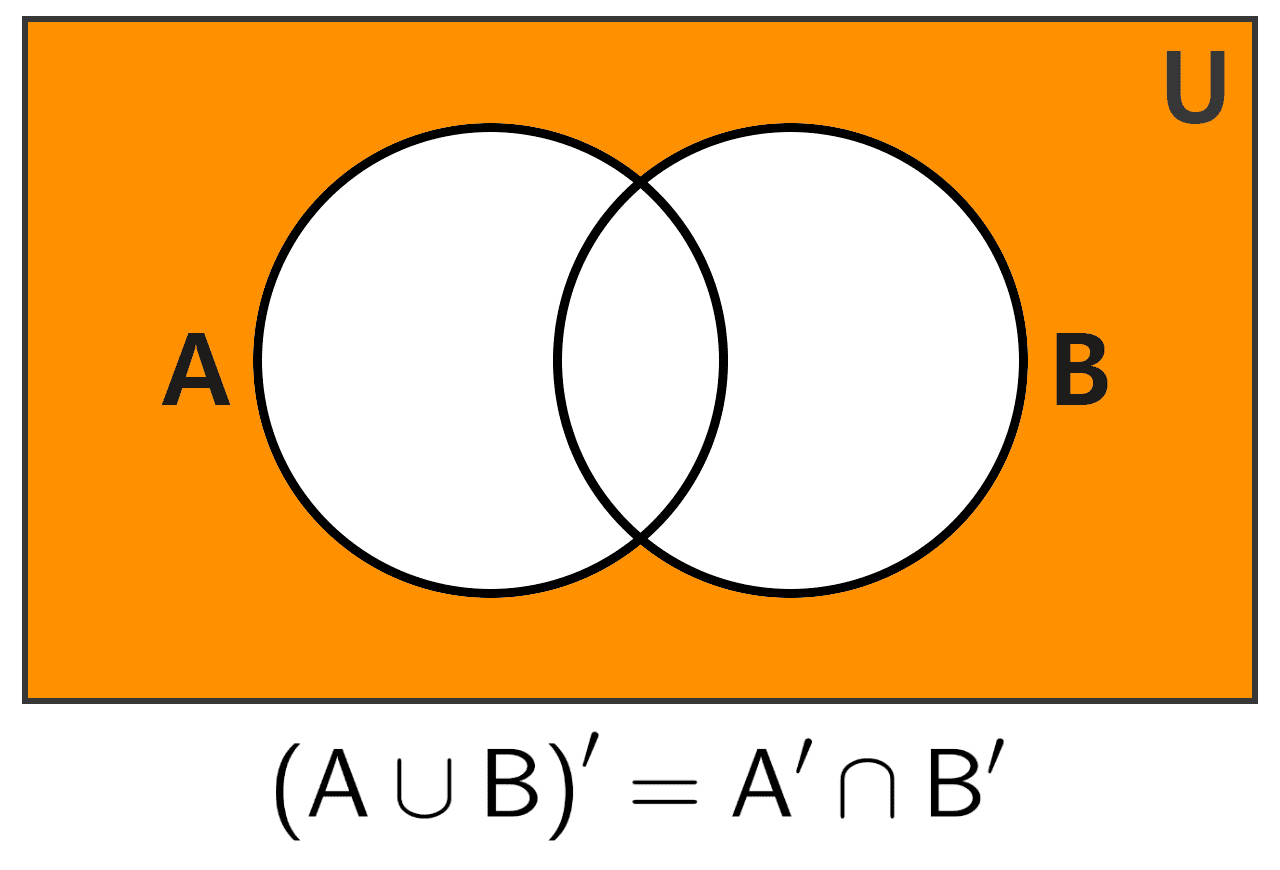
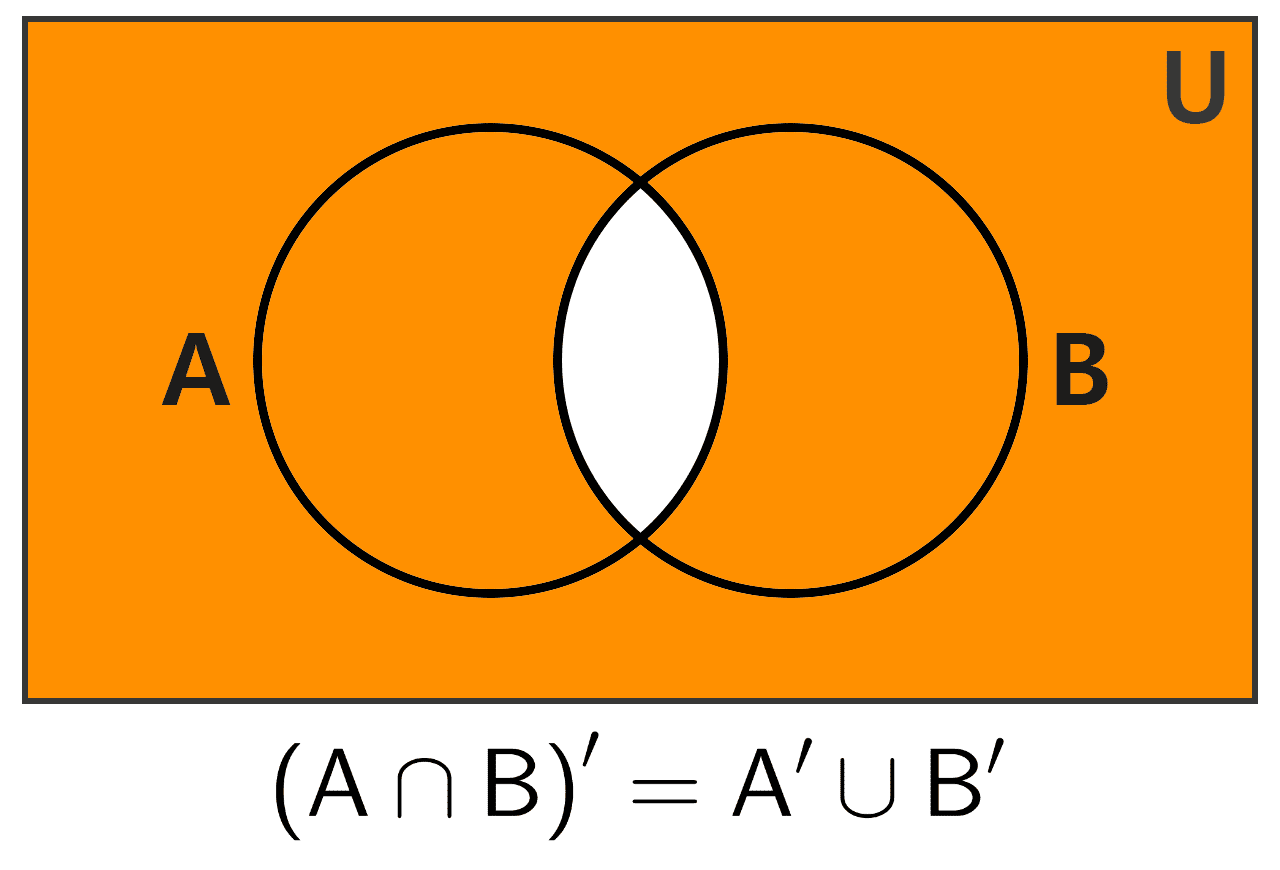




Otros artículos que te pueden interesar