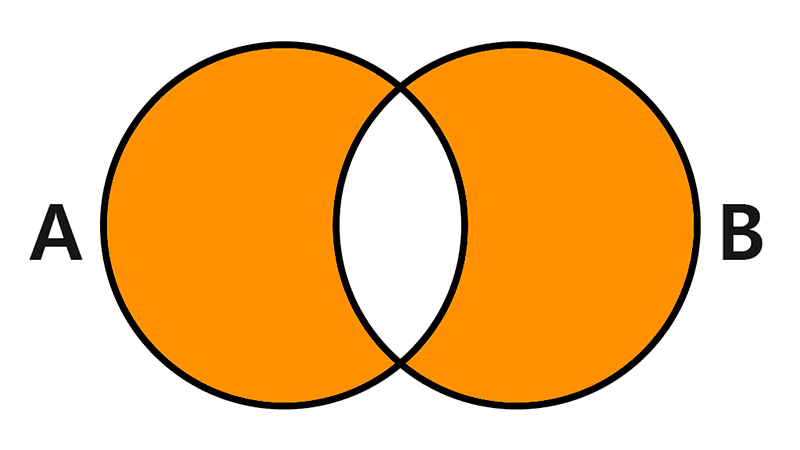
Complementación de conjuntos
La complementación de un conjunto es una operación fundamental que produce un nuevo conjunto con todos los elementos que no pertenecen al conjunto original, pero que sí están presentes dentro de un conjunto universal de referencia. El complementario de un conjunto A se representa comúnmente con una comilla simple (A′), una barra superior (Ā), o con un superíndice ‘C’ (AC).
Formalmente, si tenemos un conjunto universal U y un subconjunto A ⊆ U, el complemento de A se define como el conjunto de todos los elementos de U que no están en A, se denota como A′ y se expresa por comprensión de la siguiente manera:
A′ = { x | x ∈ U ∧ x ∉ A }
En esta definición se utilizan una conjunción y una negación lógica: un elemento formará parte del complemento si está en el universal y al mismo tiempo no está en A. Esto significa que el complemento de A es, en esencia, lo que le falta a A para ser igual al conjunto universal U.
Otra forma útil de entender esta operación es como una diferencia de conjuntos: el complemento de A no es más que la diferencia entre el conjunto universal U y el propio conjunto A. Es decir:
A′ = U - A
Esta relación podemos hallarla analizando la definición dada antes.
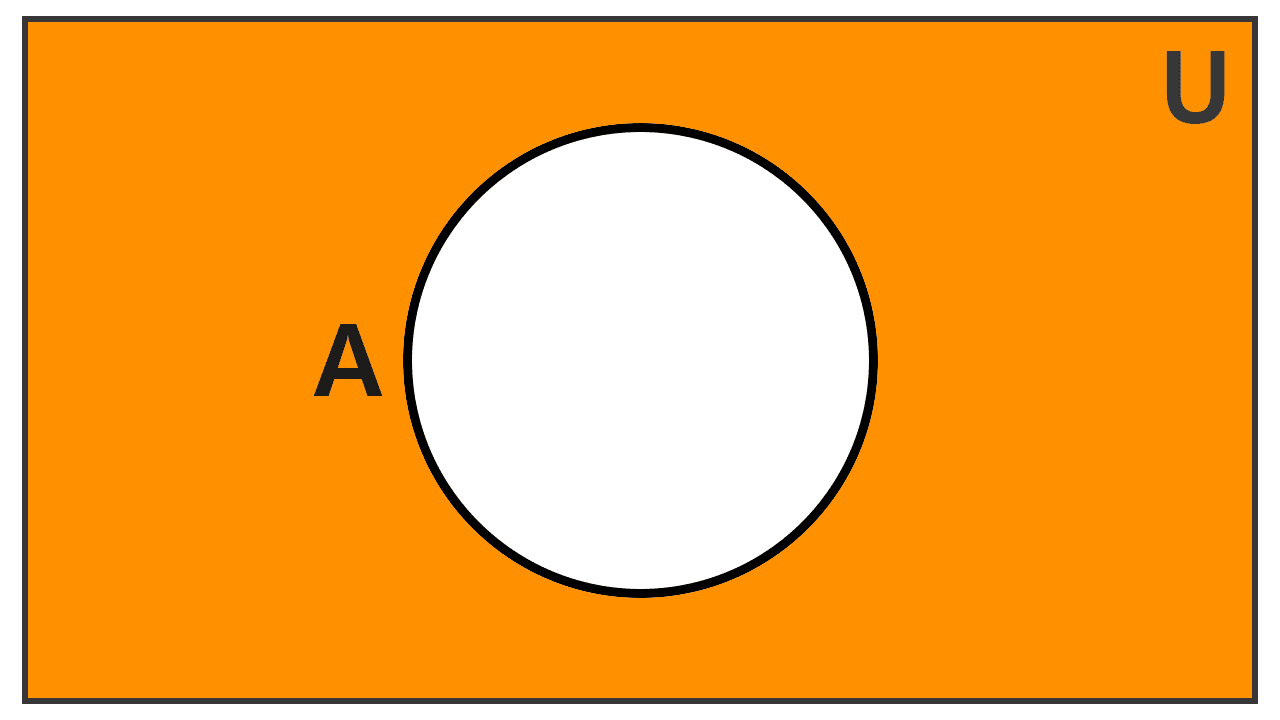
Es habitual también definir el complemento de un conjunto A relativo a otro conjunto B, lo que se conoce como diferencia de conjuntos y se denota como B - A o CBA. Este conjunto está formado por los elementos que pertenecen a B pero no a A, es decir, B actúa como el conjunto universal.
Índice
Ejemplos
Es fundamental saber que esta operación requiere que se defina explícitamente un conjunto universal U que actúe como referencia. En contextos numéricos, si no se especifica lo contrario, es habitual considerar como universal al conjunto de los números reales (R).
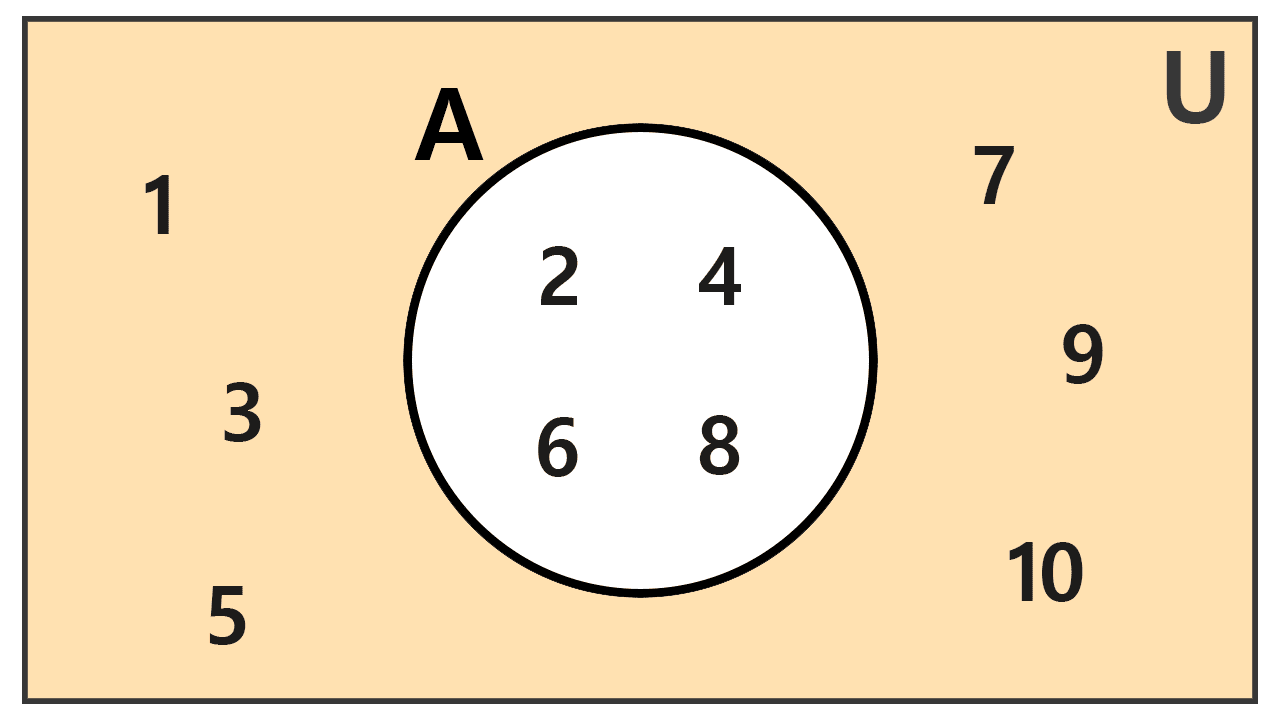
Ejemplo 1
Sean el conjunto universal U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} y el conjunto A = {2, 4, 6, 8}. Hallar el complemento de A.
Solución
El complemento de A, denotado A′, está formado por todos los elementos de U que no se encuentran en A. Procedemos listando los números del 1 al 10 y excluyendo aquellos que están en A. Así, los elementos 2, 4, 6 y 8 pertenecen a A, por lo que no formarán parte del complemento. El nuevo conjunto estará compuesto por los elementos restantes de U:
A′ = {1, 3, 5, 7, 9, 10}
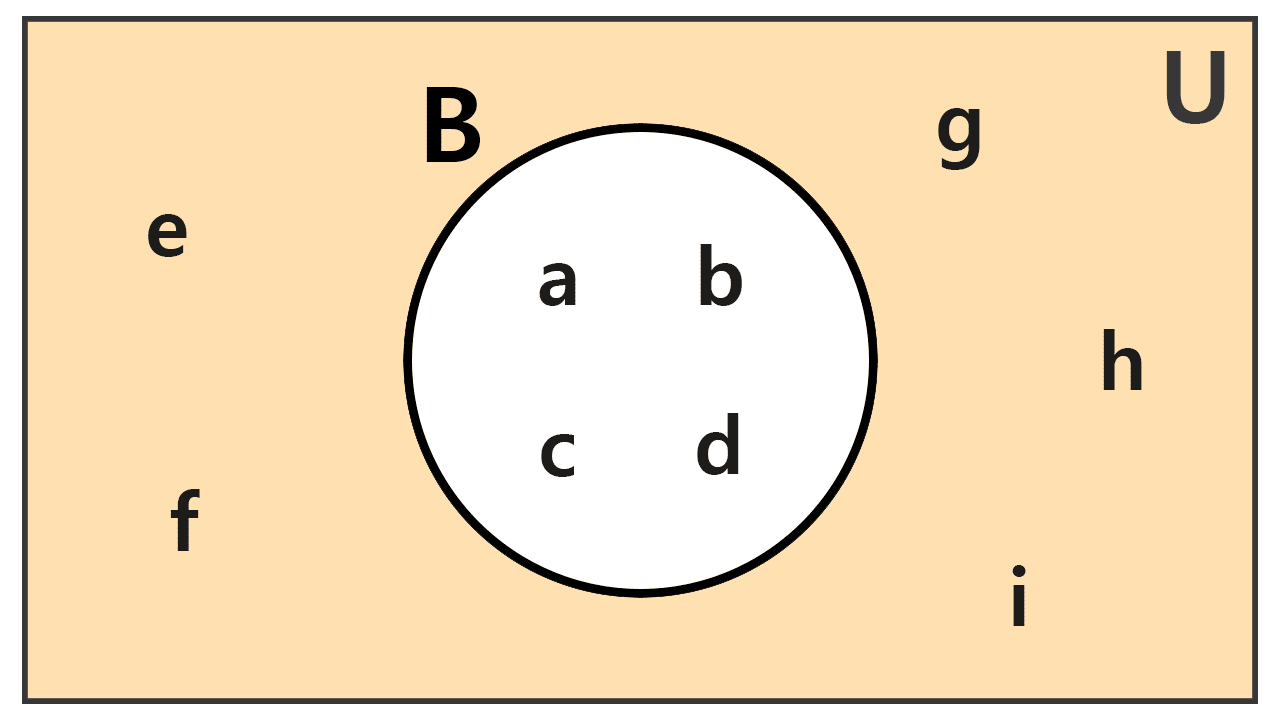
Ejemplo 2
Dado el conjunto universal formado por las letras del alfabeto español, U = {a, b, c, d, e, f, g, h, i}, y el conjunto B = {a, b, c, d}, calcular B′.
Solución
El complementario de B serán todas las letras que le faltan para llegar a ser igual al conjunto universo, es decir:
B′ = {e, f, g, h, i}
Ejemplo 3
Si tomamos como conjunto universal a los números naturales N = {1, 2, 3, ...} y definimos el conjunto P = {2, 4, 6, 8, 10, …} de los números pares positivos, encontrar P′.
Solución
El conjunto P′ estará formado por todos los números naturales que no son pares, es decir, los números impares. Por lo tanto:
P′ = {1, 3, 5, 7, ...}
Ejemplo 4
Considerando el conjunto universal de los números enteros Z, hallar el complementario del conjunto de los enteros no negativos, A = {0, 1, 2, 3, ...}.
Solución
El complementario de A en Z será el conjunto de todos los enteros que no son ni cero ni positivos. Esto corresponde exactamente al conjunto de los enteros negativos:
A′ = {-1, -2, -3, ...}
Ejemplo 5
Dentro del universo de los números reales (R), determinar el complemento del conjunto de los números racionales (Q).
Solución
El conjunto de los números racionales Q incluye todas las fracciones y decimales finitos o periódicos. Su complemento en R es el conjunto de los números que no pueden expresarse como una fracción, es decir, los números irracionales, como π o √2. Por lo tanto:
Q′ = I (el conjunto de los irracionales).
Ejemplo 6
Sea el conjunto universal U = {x ∈ Z | -5 ≤ x ≤ 5} y el conjunto F = {-2, -1, 0, 1, 2}. Calcular F′.
Solución
Primero expresamos U por extensión:
U = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5}
El complemento de F se obtiene removiendo de U los elementos de F. Así, los elementos a eliminar son -2, -1, 0, 1 y 2. El conjunto resultante es:
F′ = {-5, -4, -3, 3, 4, 5}
Propiedades
La operación de complementación en teoría de conjuntos posee una serie de propiedades fundamentales que simplifican su cálculo y la relacionan con otras operaciones.
1) Complemento del conjunto vacío: el complemento del conjunto vacío es siempre el conjunto universal. Al no haber elementos en ∅, todos los elementos de U pertenecen a su complemento.
∅′ = U
2) Complemento del conjunto universal: de manera recíproca, el complemento del conjunto universal es el conjunto vacío, ya que no existen elementos fuera de U.
U′ = ∅
3) Involución: el complemento del complemento de un conjunto es igual al conjunto original.
(A′)′ = A
4) Unión con el complemento: la unión de cualquier conjunto con su complemento siempre resulta en el conjunto universal. Juntos, contienen todos los elementos posibles de U.
A ∪ A′ = U
5) Intersección con el complemento: un conjunto y su complemento son siempre disjuntos (no comparten ningún elemento). Su intersección es, por tanto, el conjunto vacío.
A ∩ A′ = ∅
6) Leyes de De Morgan: estas leyes conectan la complementación con la unión y la intersección, mostrando cómo actúa el complemento sobre estas operaciones.
El complemento de una unión es igual a la intersección de los complementos:
(A ∪ B)′ = A′ ∩ B′
El complemento de una intersección es igual a la unión de los complementos:
(A ∩ B)′ = A′ ∪ B′
7) Subconjuntos: si un conjunto A es subconjunto de B, entonces el complemento de B es subconjunto del complemento de A:
Si A ⊆ B, entonces B′ ⊆ A′.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

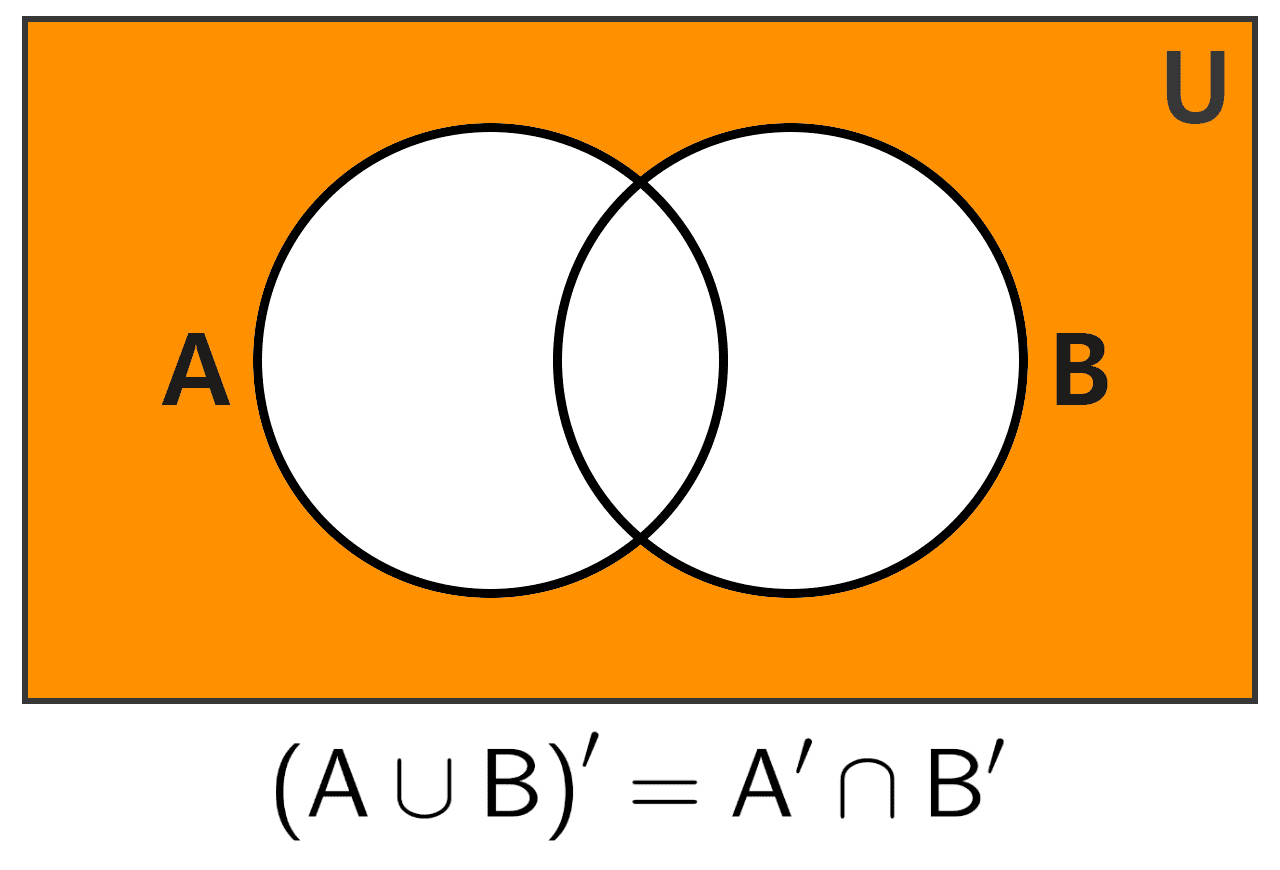
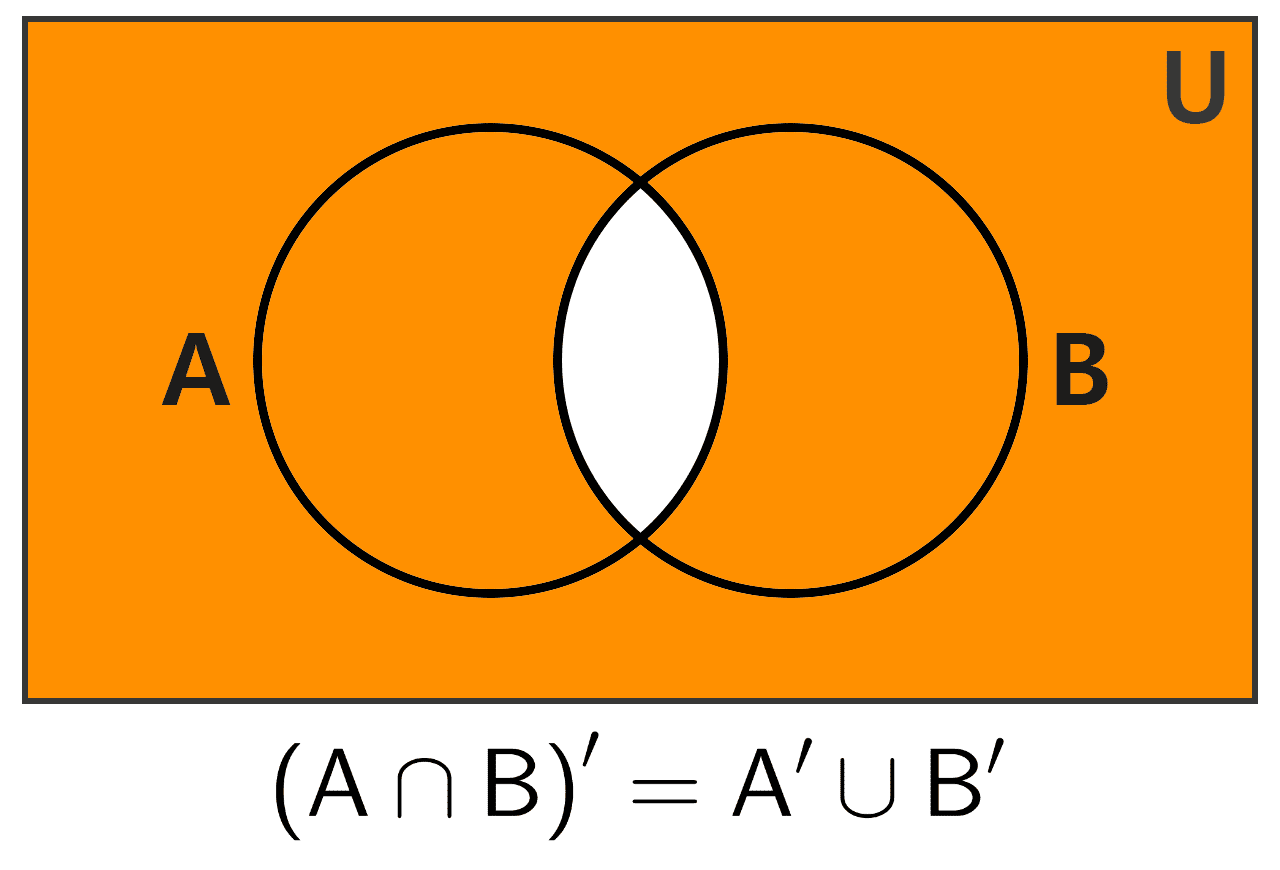
Otros artículos que te pueden interesar