
Unión de conjuntos
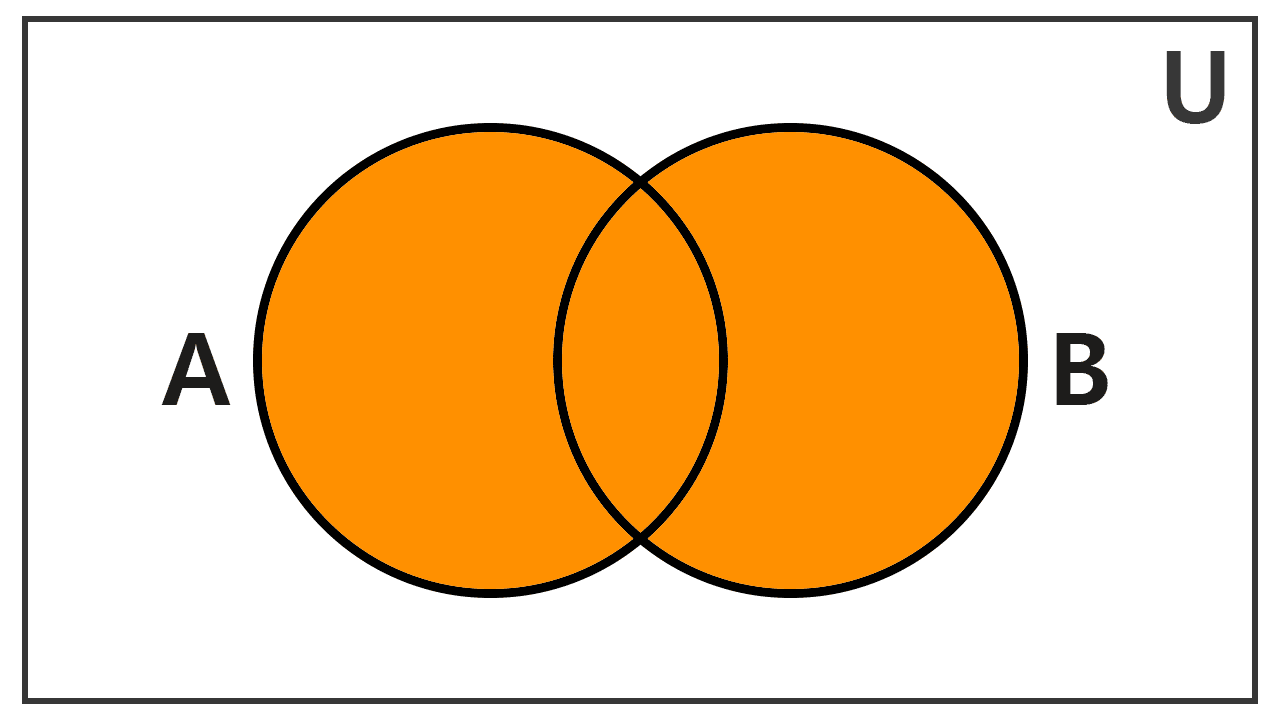
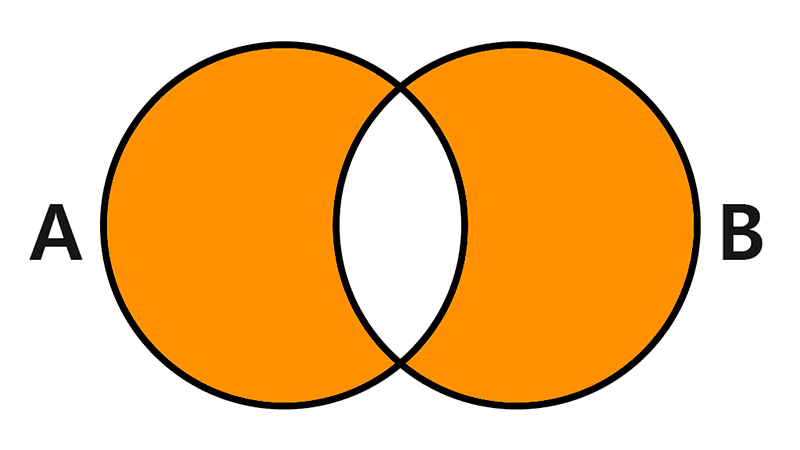
La unión de conjuntos es una operación que crea un nuevo conjunto que contiene todos los elementos de los conjuntos originales, sin repetir los elementos comunes. Se representa con el símbolo “∪”, similar a la letra U.
Formalmente, definimos la unión de dos conjuntos A y B como el conjunto formado por los elementos que pertenecen a A, a B o a ambos. Se denota como A ∪ B y se expresa por comprensión como:
A ∪ B = { x | x ∈ A ∨ x ∈ B }
Vemos que en la definición se utiliza una disyunción inclusiva (el conectivo lógico "o"), y es por eso que un elemento formará parte de la unión si pertenece a uno de los conjuntos o a ambos simultáneamente.
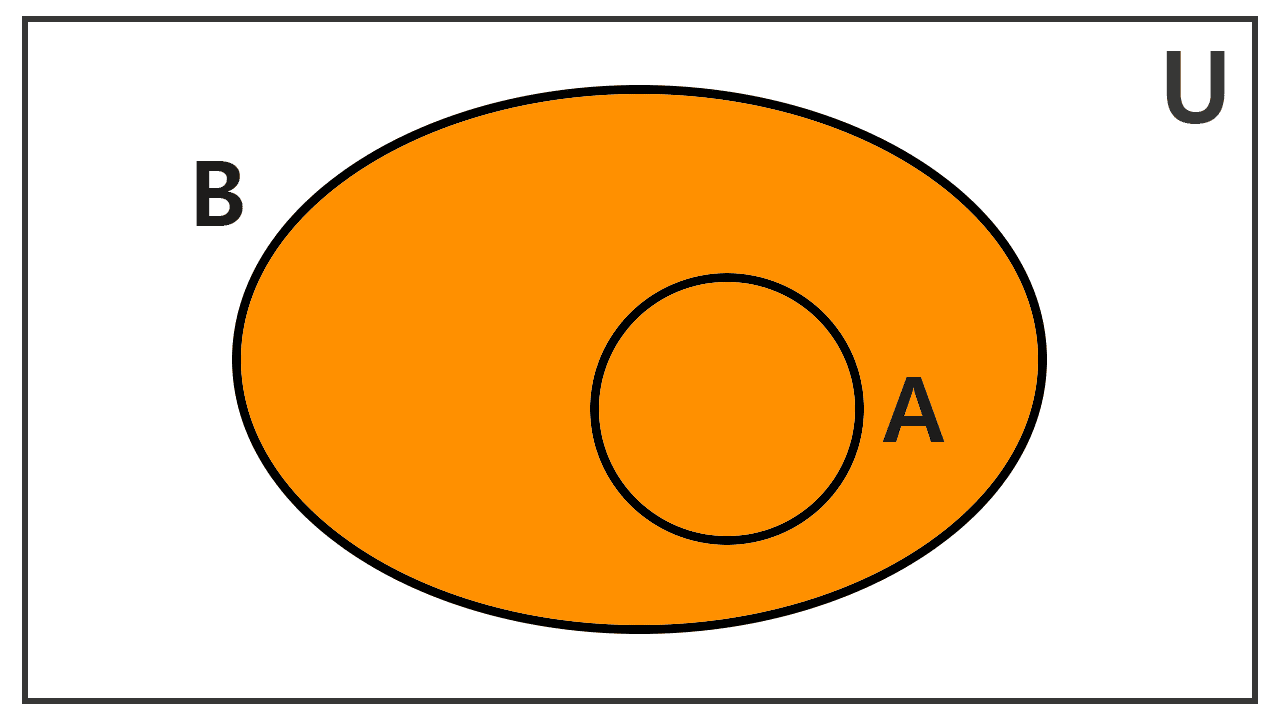
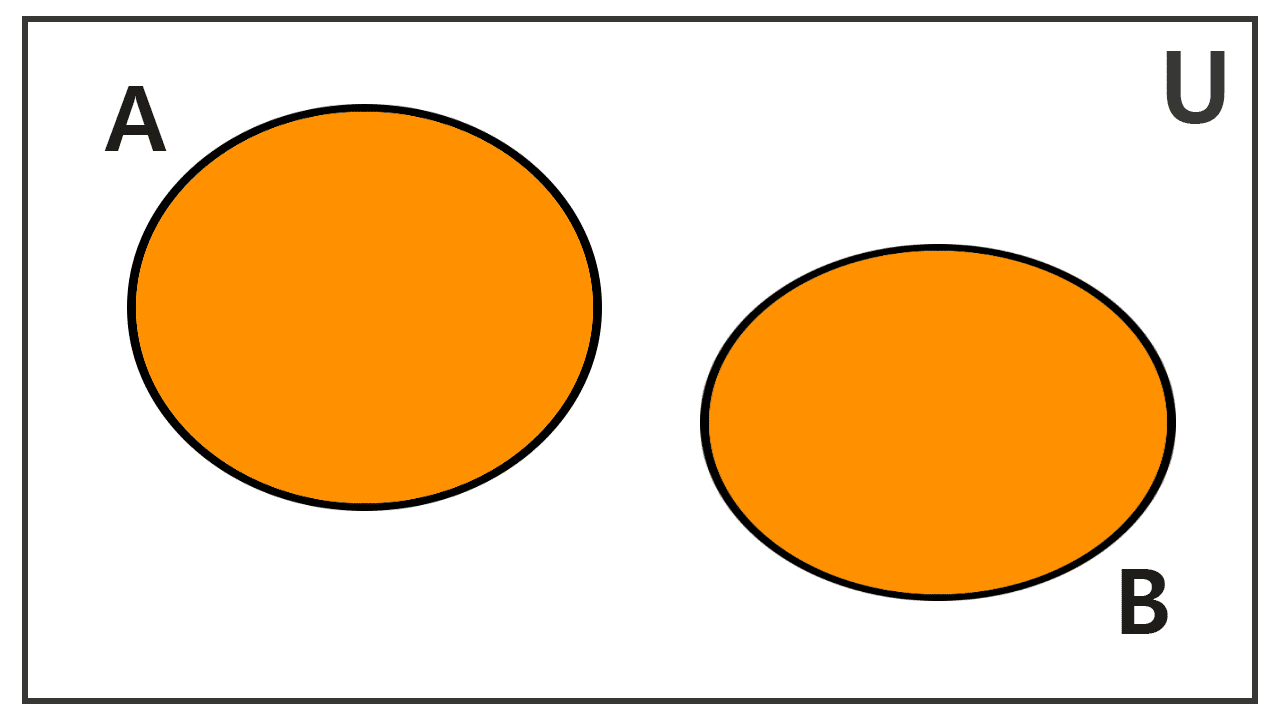
Los diagramas de Venn nos permiten visualizar esta operación. Aunque los conjuntos pueden relacionarse de distintas maneras, podemos ilustrar la unión considerando tres situaciones fundamentales.
La diferencia fundamental entre la unión y la intersección de conjuntos reside en los elementos que incluye cada una: la unión de dos conjuntos agrupa todos los elementos que pertenecen a al menos uno de ellos; en cambio, la intersección se limita exclusivamente a los elementos que comparten los conjuntos involucrados.
Índice
Ejemplos
A continuación veremos algunos ejemplos de unión de conjuntos. Es importante destacar que si existen elementos repetidos, en la unión se escribirán solo una vez.
Ejemplo 1
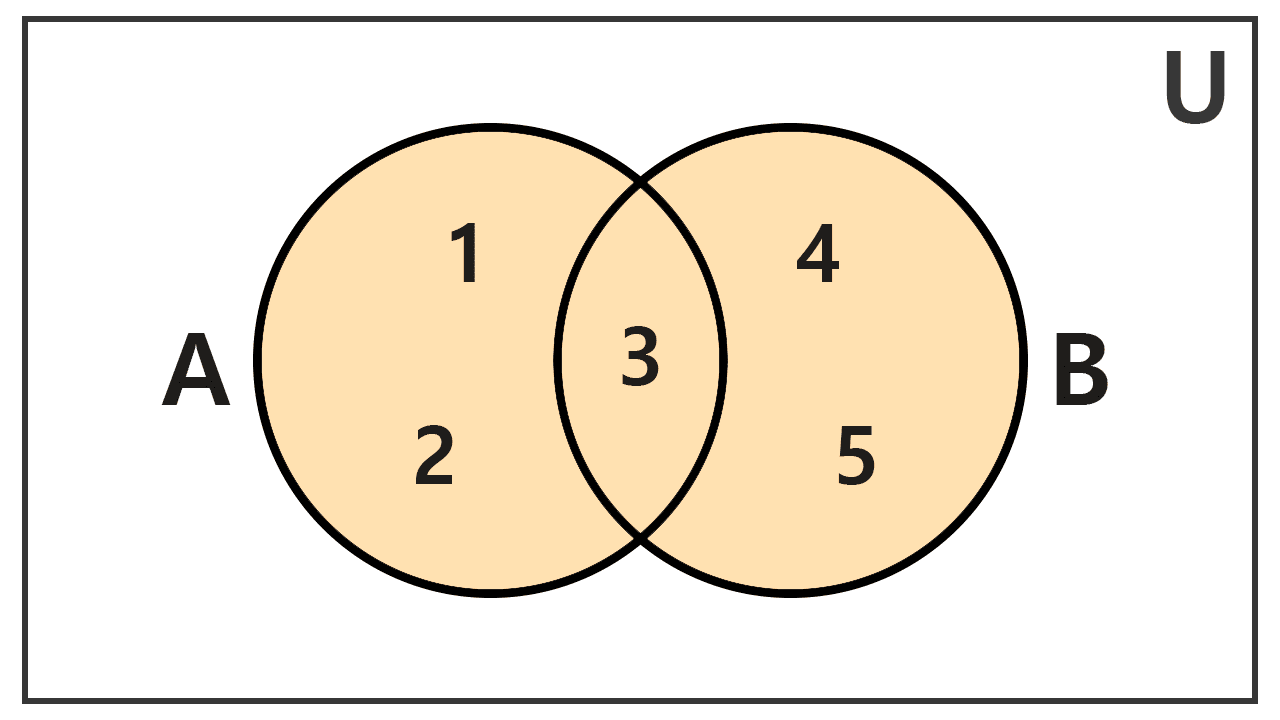
Sean A = {1, 2, 3} y B = {3, 4, 5}, calcular su unión.
Solución
Para resolver la unión de dos conjuntos, combinamos todos los elementos que pertenecen a A o a B. Observamos que el elemento 3 está presente en ambos conjuntos. Sin embargo, en la unión, los elementos repetidos se incluyen una sola vez. Por lo tanto, al unir A y B, obtenemos el conjunto:
A ∪ B = {1, 2, 3, 4, 5}
Ejemplo 2
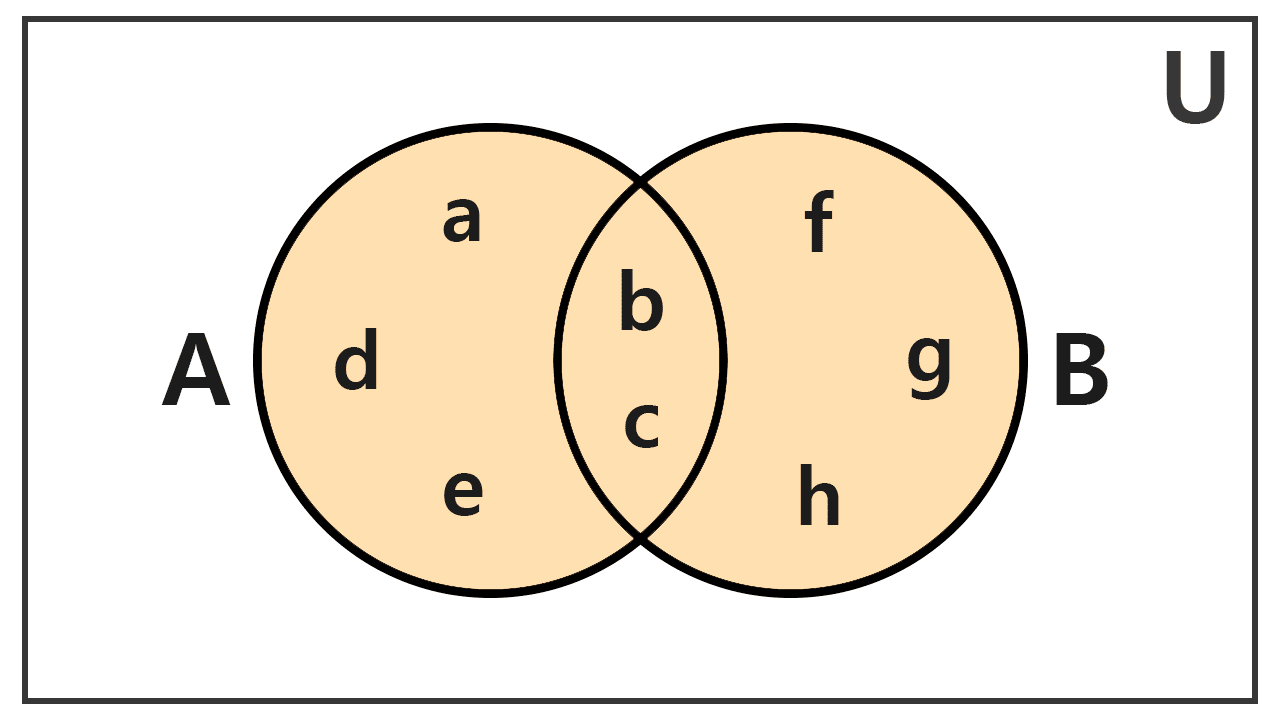
Determinar el conjunto resultante de la unión entre A = {a, b, c, d, e} y B = {b, c, f, g, h}.
Solución
Al realizar la unión de estos dos conjuntos, reunimos todos sus elementos. Los elementos 'b' y 'c' son comunes a ambos, por lo que solo los consideramos una vez. El conjunto unión queda entonces de la siguiente forma:
A ∪ B = {a, b, c, d, e, f, g, h}
Ejemplo 3
Encontrar la unión de los conjuntos C = {-1, -2, -3} y D = {1, 2, 3}.
Solución
En este caso, los conjuntos C y D no comparten ningún elemento; son conjuntos disjuntos. La unión de dos conjuntos disjuntos simplemente agrupa todos los elementos de ambos. Por lo tanto, la unión es:
C ∪ D = {-1, -2, -3} ∪ {1, 2, 3} = {-1, -2, -3, 1, 2, 3}
Ejemplo 4
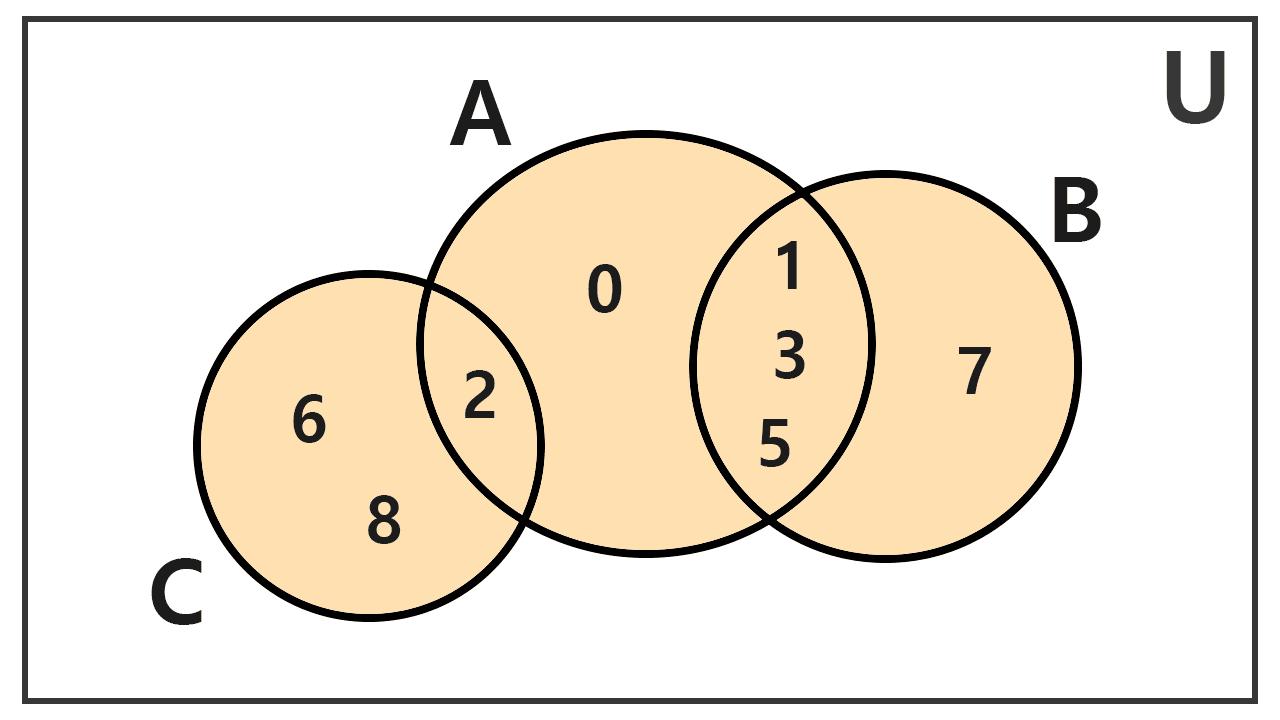
Hallar la unión de los conjuntos A, B y C, siendo A = {0, 1, 2, 3, 5}, B = {1, 3, 5, 7} y C = {2, 6, 8}.
Solución
Para calcular la unión de tres conjuntos, podemos proceder de forma escalonada. Primero, unimos A y B:
A ∪ B = {0, 1, 2, 3, 5, 7}
A continuación, unimos este resultado con el conjunto C:
(A ∪ B) ∪ C = {0, 1, 2, 3, 5, 7} ∪ {2, 6, 8}
El elemento 2 se repite, pero se cuenta una sola vez. El conjunto unión final es:
A ∪ B ∪ C = (A ∪ B) ∪ C = {0, 1, 2, 3, 5, 6, 7, 8}
Nota: el orden de unión es arbitrario, podríamos haber unido primero A con C (o B con C) y el resultado sería el mismo. Esto se debe a las propiedades de asociatividad y conmutatividad de esta operación.
Ejemplo 5
Resolver la unión de tres conjuntos J, K y L, donde J = {1, 2, 3, 4, 5, 6}, K = {1, 3, 5, 7} y L = {2, 4, 6, 8}.
Solución
Comenzamos uniendo J y K:
J ∪ K = {1, 2, 3, 4, 5, 6, 7}
Luego, unimos este nuevo conjunto con L:
(J ∪ K) ∪ L = {1, 2, 3, 4, 5, 6, 7} ∪ {2, 4, 6, 8}
Los elementos 2, 4 y 6 ya estaban presentes, así que el conjunto unión final de los tres conjuntos es:
J ∪ K ∪ L = (J ∪ K) ∪ L = {1, 2, 3, 4, 5, 6, 7, 8}
Ejemplo 6
Resolver la unión de A, B, C y D, donde A = {1, 2}, B = {1}, C = {4, 5} y D = {-1, 0}.
Solución
Comenzamos uniendo A con el conjunto unitario B:
A ∪ B = {1, 2} ∪ {1} = {1, 2}
Luego, unimos este resultado con C:
(A ∪ B) ∪ C = {1, 2} ∪ {4, 5} = {1, 2, 4, 5}
Finalmente, unimos el conjunto anterior con D para obtener la unión de cuatro conjuntos:
((A ∪ B) ∪ C) ∪ D = {1, 2, 4, 5} ∪ {-1, 0}
Como no hay elementos repetidos entre estos conjuntos, el resultado final es la agrupación de todos los elementos:
A ∪ B ∪ C ∪ D = {-1, 0, 1, 2, 4, 5}
Ejemplo 7
Encontrar la unión de los conjuntos S = {x ∈ N | x < 10} y T = {x ∈ N | 2x ≤ 20}.
Solución
Los conjuntos están dados por comprensión, es útil expresar ambos por extensión para visualizar sus elementos. El conjunto S son los números naturales menores que 10:
S = {1, 2, 3, 4, 5, 6, 7, 8, 9}
El conjunto T incluye los números naturales para los cuales 2x ≤ 20, es decir, x ≤ 10, por lo que T = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Vemos que T tiene un elemento más que S, el “10”. La unión resulta en:
S ∪ T = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Ejemplo 8
Sean P el conjunto de los números naturales pares e I el conjunto de los números naturales impares. Encontrar P ∪ I.
Solución
El conjunto P contiene todos los números pares: P = {2, 4, 6, …}; y el conjunto I todos los impares: I = {1, 3, 5, 7, …}. No existe ningún número natural que sea a la vez par e impar, por lo que son conjuntos disjuntos. Su unión abarca entonces todos y cada uno de los números naturales. Por lo tanto, P ∪ I es igual al conjunto de los números naturales, N.
Propiedades
La operación de unión en teoría de conjuntos cumple una serie de propiedades fundamentales que nos ayudan a simplificar su cálculo. Veremos las más importantes a continuación.
1) Propiedad conmutativa: el orden en que se unan los conjuntos no altera el resultado.
A ∪ B = B ∪ A
2) Propiedad asociativa: la forma en que se agrupen los conjuntos para realizar la unión no afecta el resultado final.
(A ∪ B) ∪ C = A ∪ (B ∪ C)
3) Idempotencia: la unión de un conjunto consigo mismo es el mismo conjunto.
A ∪ A = A
4) Propiedad de identidad (o elemento neutro): la unión de cualquier conjunto con el conjunto vacío es el conjunto original.
A ∪ ∅ = A
5) Propiedad de dominación: la unión de cualquier conjunto con el conjunto universal es el conjunto universal.
A ∪ U = U
6) Distributividad respecto a la intersección: la unión de un conjunto con la intersección de otros dos es igual a la intersección de las uniones del primer conjunto con cada uno de los otros.
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
7) Ley de De Morgan: el complemento de la unión de conjuntos es igual a la intersección de sus complementos.
(A ∪ B)’ = A’ ∩ B’
8) Cardinalidad: el número de elementos de la unión de dos conjuntos finitos es la suma de sus elementos menos la cantidad de elementos que comparten (su intersección).
|A ∪ B| = |A| + |B| - |A ∩ B|
9) Propiedades relacionadas con los subconjuntos:
- Si dos conjuntos son subconjunto de un tercero, su unión también es subconjunto de él: si A ⊆ C y B ⊆ C, entonces A ∪ B ⊆ C.
- Si un conjunto es subconjunto de otro, la unión de ambos es igual al conjunto contenedor: si A ⊆ B, entonces A ∪ B = B.
- Si un conjunto está incluido en dos conjuntos a la vez, entonces también está incluido en su unión: si X ⊆ A y X ⊆ B, entonces X ⊆ A ∪ B.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

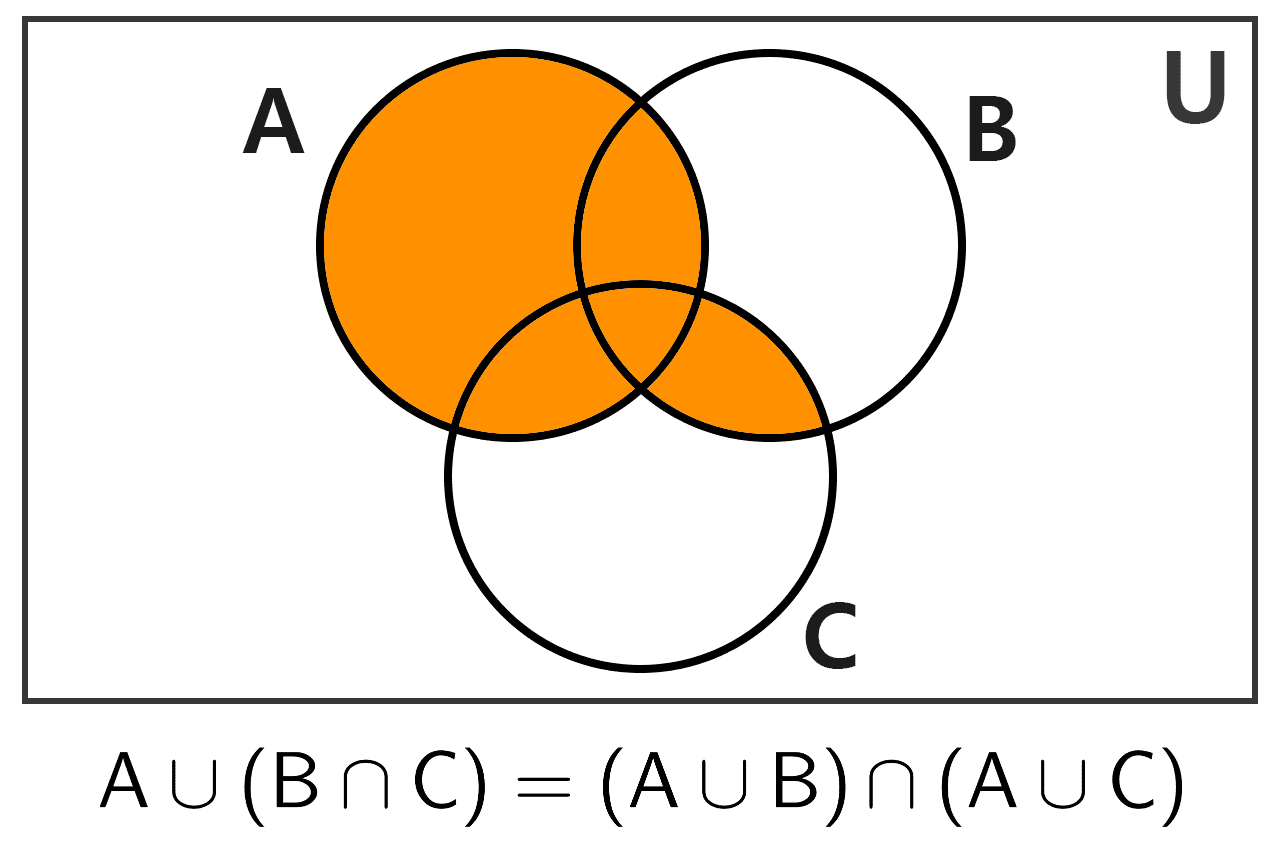
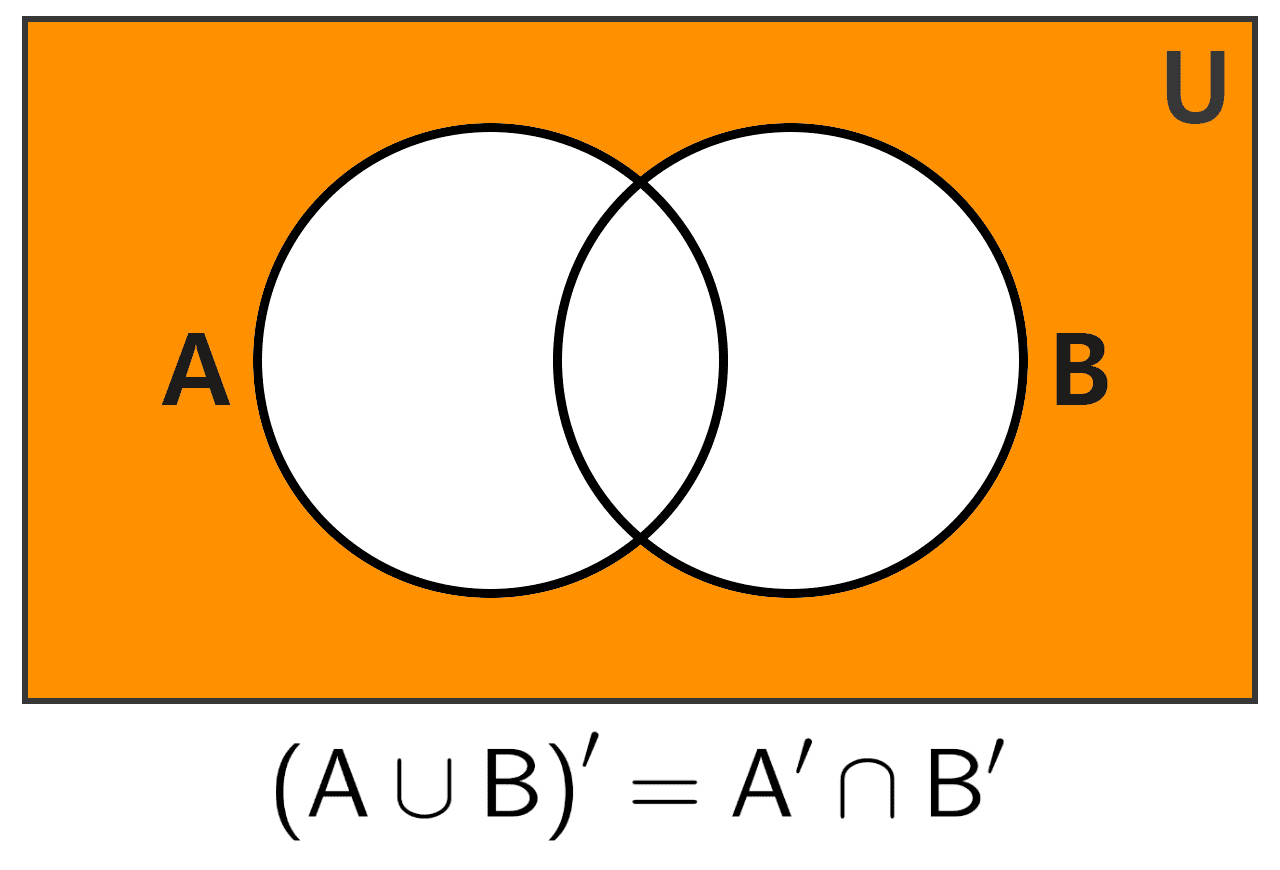
Otros artículos que te pueden interesar