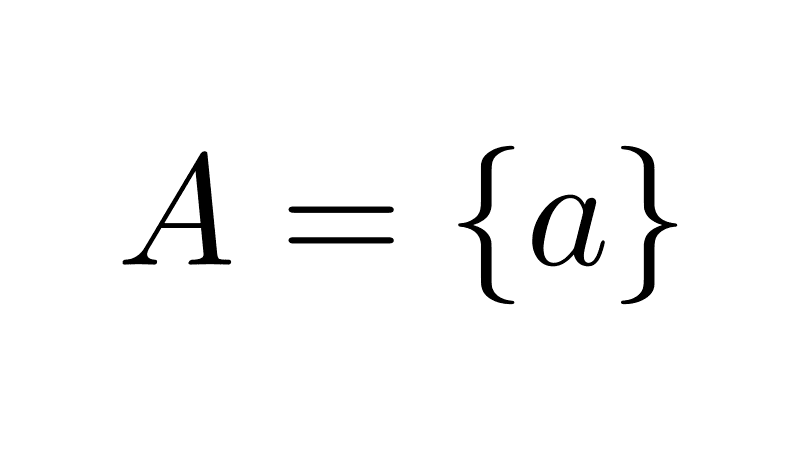
¿Qué es un conjunto en matemáticas?
Un conjunto es una colección o agrupación bien definida de objetos, a los que se les llama elementos. Estos objetos pueden ser de carácter concreto (personas, animales, objetos materiales, etc.) o de carácter abstracto (números, ideas, conceptos, relaciones, etc.). La característica esencial de un conjunto es que está claramente determinado qué elementos lo componen y cuáles no.
Un ejemplo sencillo de colección bien definida es "el conjunto de los días de la semana": sabemos con certeza que "lunes" pertenece al conjunto, pero "marzo" no. En cambio, si hablamos de "el conjunto de las canciones bonitas", no podemos determinarlo con precisión porque depende del gusto de cada persona, por lo que no constituye un conjunto matemático válido.
La noción de pertenencia es clave en la teoría de conjuntos: un elemento puede pertenecer o no pertenecer a un conjunto. Para expresarlo, se utilizan símbolos específicos: si el elemento a pertenece al conjunto A, se escribe a ∈ A; en cambio, si no pertenece, se escribe a ∉ A.
En matemáticas, los conjuntos suelen representarse con letras mayúsculas (A, B, C, …), mientras que los elementos se denotan con letras minúsculas (a, b, c, …). Es importante destacar que, dentro de un mismo conjunto, los elementos son únicos (no se repiten) y el orden en que se escriban no altera el conjunto. Por ejemplo, los conjuntos {1, 2, 3}, {1, 1, 2, 2, 3} y {3, 1, 2} representan exactamente lo mismo.
Aunque en principio un conjunto puede contener elementos de cualquier naturaleza, incluso heterogéneos (como un número, un color y un animal en un mismo conjunto), en matemáticas se emplean principalmente para organizar y clasificar objetos que comparten propiedades comunes. Esto permite trabajar con ellos de manera estructurada, establecer relaciones entre diferentes colecciones y realizar operaciones entre ellas.
Índice
Cómo se representan los conjuntos
Expresar los elementos que conforman un conjunto se conoce como determinar el conjunto. En matemáticas existen dos maneras principales de hacerlo en forma escrita: por extensión, listando cada elemento, o por comprensión, indicando la característica que comparten los elementos. Además de estas formas escritas, los conjuntos también pueden representarse de manera visual mediante diagramas de Venn, que permiten ilustrar gráficamente la relación entre diferentes conjuntos.
Representación por extensión (o enumeración)
Consiste en escribir explícitamente todos los elementos que conforman el conjunto, separados por comas y encerrados entre llaves { }.
Un aspecto importante que ya mencionamos antes es que el orden de los elementos no importa y que los elementos no se repiten. Por ejemplo, los conjuntos {a, b, c}, {c, a, b} y {a, b, b, c} representan exactamente lo mismo.
Ejemplos
- A = {a, b, c} es el conjunto de las tres primeras letras del alfabeto.
- B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} es el conjunto de los primeros diez números naturales.
- C = {-1, 1} es el conjunto formado por los números -1 y 1.
- D = {n, d, m, u, o} es el conjunto de letras que forman la palabra "mundo".
- E = {primavera, verano, otoño, invierno} es el conjunto de las estaciones del año.
La representación por extensión es clara y sencilla, pero solo resulta práctica cuando el conjunto tiene un número finito y pequeño de elementos.
Representación por comprensión (o propiedad)
En lugar de listar uno por uno los elementos, se describe la propiedad o condición común que todos cumplen. Para ello se utiliza la notación:
{ x | x cumple una propiedad }
Esto se lee como "el conjunto de todos los x tales que x cumple cierta propiedad".
Ejemplos
- P = { x | x es un número entero y par } es el conjunto de todos los números enteros pares.
- R = { x | x es un número real } es el conjunto de todos los números reales.
- { x | x es real y x ≥ 6 } es el conjunto de todos los números reales mayores o iguales a 6.
- Q = { x | x es un cuadrado de un número natural } es conjunto de todos los números que son cuadrados perfectos.
- V = { x | x es una vocal del alfabeto español } es el conjunto de vocales.
La ventaja de esta forma es que permite describir conjuntos infinitos o muy grandes, que no podrían listarse por extensión.
Representación mediante diagramas de Venn
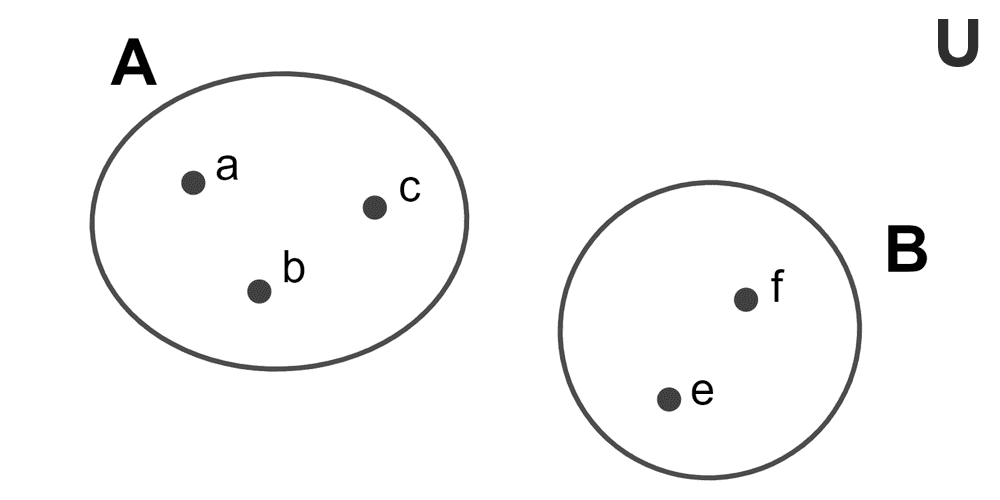
Los diagramas de Venn son representaciones gráficas que permiten visualizar conjuntos y sus relaciones. Se dibuja un rectángulo para el conjunto universal (todos los elementos posibles en el contexto) y dentro de él, círculos u óvalos que representan los conjuntos particulares.
Por ejemplo: sean los conjuntos A = {a, b, c} y B = {e, f}, en el diagrama se representan como dos círculos distintos dentro del rectángulo universal, sin intersección entre ellos.
Tipos de conjuntos
Existen diferentes clases de conjuntos, algunas de estas son:
- Conjunto finito: es aquel que tiene un número limitado de elementos, de modo que podemos contarlos todos. Por ejemplo, el conjunto de los meses del año es finito porque contiene doce elementos.
- Conjunto infinito: es aquel que no tiene un límite en la cantidad de elementos y, por lo tanto, no podemos contarlos en su totalidad. Un ejemplo es el conjunto de los números reales, que se extiende indefinidamente tanto hacia los positivos como hacia los negativos.
- Conjunto vacío (∅): es un conjunto que no contiene ningún elemento. Se representa con el símbolo ∅ o con llaves vacías {}. Un ejemplo es el conjunto de los números impares que son divisibles por 2, ya que no existe ningún número que cumpla esa condición.
- Conjunto universal (U): es el conjunto que reúne a todos los elementos que son relevantes dentro de un contexto específico y sirve como marco de referencia para definir otros conjuntos. Por ejemplo, si estamos trabajando con las vocales, el conjunto universal podría ser el abecedario completo.
Relaciones entre elementos y conjuntos
Hasta ahora hemos hablado de la relación de pertenencia, que conecta a un elemento con un conjunto. Sin embargo, los conjuntos también pueden relacionarse entre sí, y una de las formas más importantes es a través de la inclusión. A continuación veremos ambas relaciones con más detalle.
- Relación de pertenencia: un elemento pertenece a un conjunto si forma parte de él, lo cual se indica con el símbolo ∈. Por ejemplo, si V = {a, e, i, o, u}, entonces a ∈ V porque la letra "a" está dentro de V, mientras que b ∉ V porque "b" no forma parte del conjunto de vocales.
- Relación de inclusión: se dice que un conjunto A es subconjunto de B, escrito A ⊆ B, cuando todos los elementos de A también pertenecen a B. Así, si A = {1, 2} y B = {1, 2, 3, 4}, entonces A ⊆ B porque cada elemento de A se encuentra en B. Cuando A está incluido en B pero además A ≠ B, se habla de subconjunto propio, simbolizado como A ⊂ B.
Operaciones entre conjuntos
Los conjuntos se pueden combinar mediante distintas operaciones, lo que permite construir nuevas colecciones a partir de otras y analizar cómo interactúan. Las más comunes son:
- Unión (∪): la unión de dos conjuntos A y B es el conjunto de todos los elementos que están en A, en B o en ambos. Se define como A ∪ B = {x | x ∈ A o x ∈ B}. Por ejemplo, {1, 2} ∪ {2, 3} = {1, 2, 3}.
- Intersección (∩): la intersección de A y B está formada por los elementos que pertenecen simultáneamente a ambos conjuntos, se escribe A ∩ B = {x | x ∈ A y x ∈ B}. Por ejemplo, {1, 2} ∩ {2, 3} = {2}.
- Diferencia (–): la diferencia A – B es el conjunto de elementos que pertenecen a A pero no a B. Se expresa como A – B = {x | x ∈ A y x ∉ B}. Por ejemplo, {1, 2} – {2, 3} = {1}.
- Complementación: el complemento de un conjunto A, respecto de un conjunto universal U, se define como Ac = {x | x ∈ U y x ∉ A}. Así, si U = {1, 2, 3, 4, 5} y A = {2, 4}, entonces Ac = {1, 3, 5}.
Bibliografía
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.
- Wilches, L., Costa, R., Rincón, M., Acosta, M., Roa, J., Sulvara, J. y Jaime, D. (2013). Matemática 6. Editorial Santillana.
- Zill, D. y Dewar, J. (2012). Álgebra, trigonometría y geometría analítica (3ra edición). McGraw Hill.
¡Suscríbete a Flamath!
Recibe contenido exclusivo y sé el primero en enterarte de nuestras novedades.
Deja una respuesta


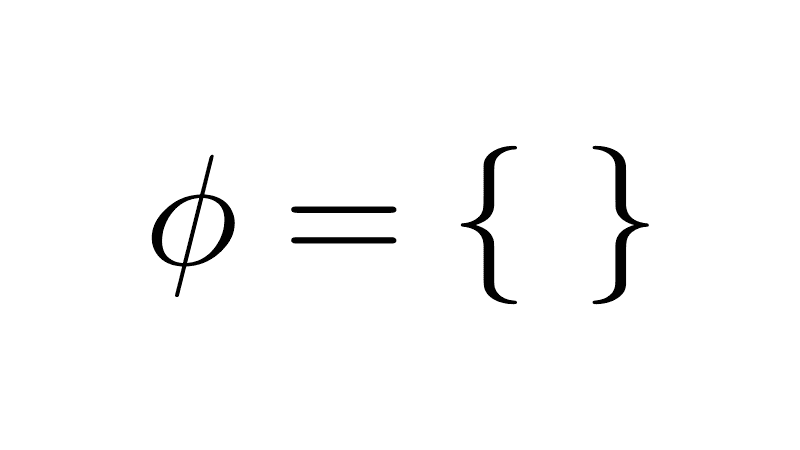
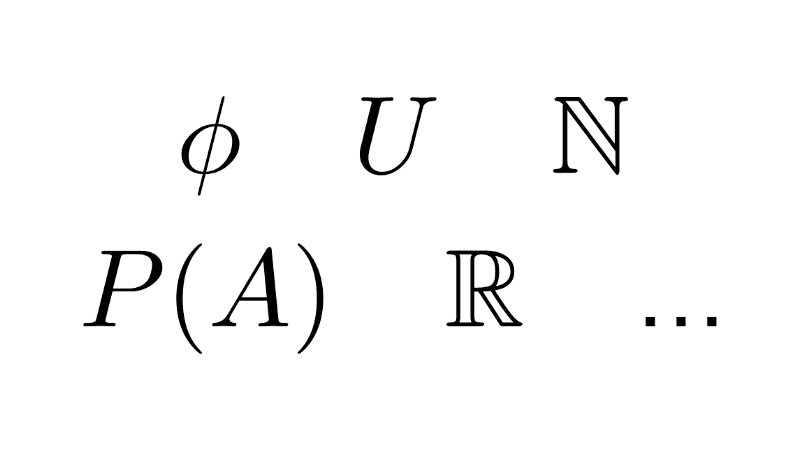
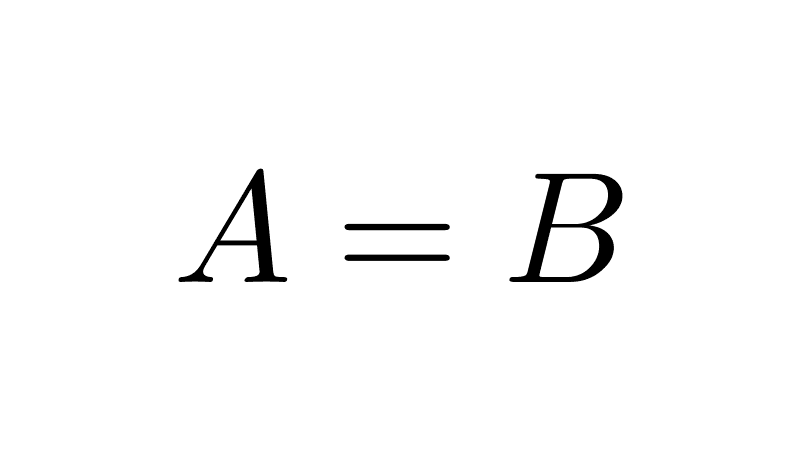
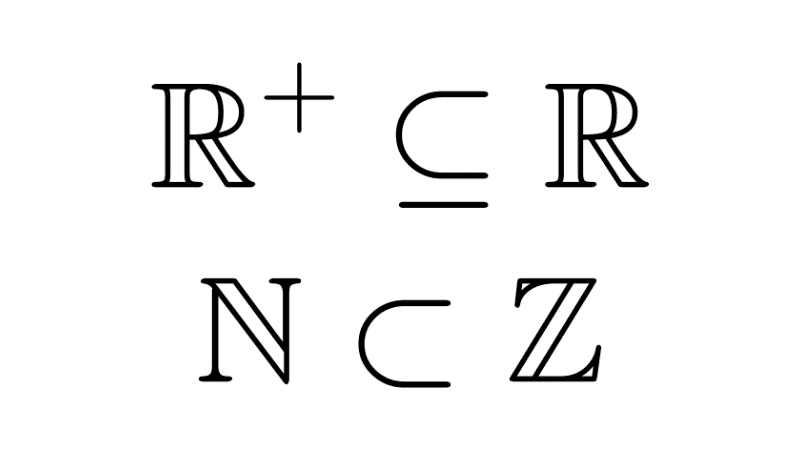
Otros artículos que te pueden interesar