Ejercicios resueltos de lógica proposicional
Aquí encontrarás problemas de lógica proposicional resueltos paso a paso para todos los niveles educativos.
Índice
Fundamentos
Te recomiendo revisar estos artículos para repasar los conceptos básicos de la lógica proposicional y ver ejercicios comunes resueltos:
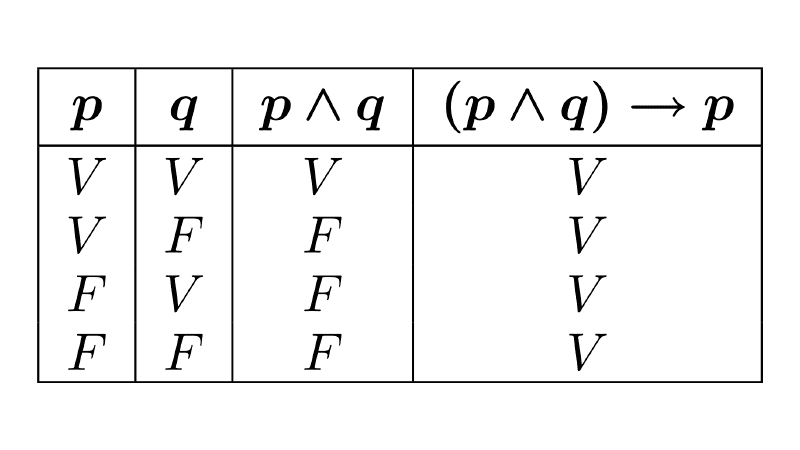
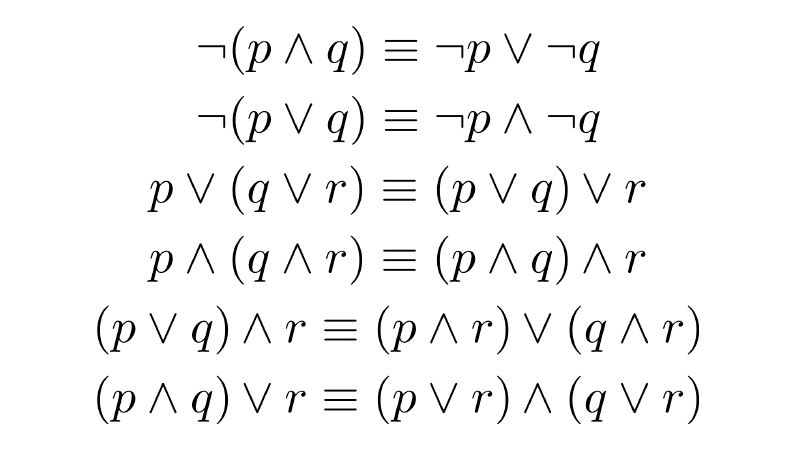
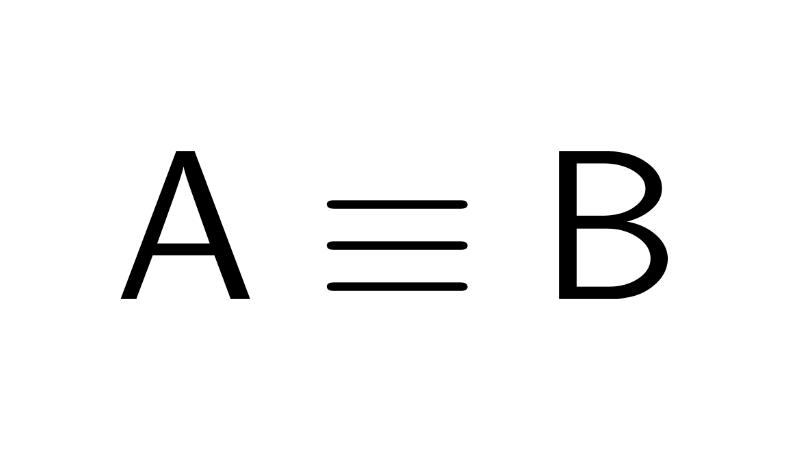





Tipos de proposiciones y fórmulas bien formadas
Ejercicio 1
Determinar cuáles de las siguientes expresiones son proposiciones; en los casos que sí sea, clasificarla como simple o compuesta.
- La capital de Perú es Lima.
- x + 5 = 10.
- No es cierto que el Sol gira alrededor de la Tierra.
- El número 7 es un número primo y el 6 es compuesto.
- ¿Qué edad tienes?
- Si llueve, entonces tendremos buena cosecha.
- ¡Cierra la puerta inmediatamente!
- O estudias para el examen o reprobarás la materia.
- Ojalá mañana sea un día soleado.
- Lava los platos y seca los cubiertos.
- 9 < 5.
- ¡Dame una mano con esto, por favor!
- El número 2 es par o el número 3 es impar.
Soluciones
a) Analizando la oración "La capital de Perú es Lima", identificamos que es una declaración con un valor de verdad definido (verdadero), por lo tanto es una proposición simple.
b) La expresión "x + 5 = 10" contiene una variable (x), por lo que su valor de verdad no puede determinarse sin asignarle un valor; por consiguiente, no es una proposición.
c) La frase "No es cierto que el Sol gira alrededor de la Tierra" es una declaración que niega una afirmación; posee un valor de verdad definido (verdadero) y es una proposición compuesta (negación).
d) "El número 7 es un número primo y el 6 es compuesto" es una declaración compuesta por dos proposiciones simples unidas por el conectivo "y"; tiene un valor de verdad definido (verdadero) y es una proposición compuesta (conjunción).
e) La expresión "¿Qué edad tienes?" es una pregunta, no afirma ni niega nada, por lo tanto no es una proposición.
f) "Si llueve, entonces tendremos buena cosecha" es una declaración condicional compuesta por dos proposiciones; tiene un valor de verdad definido (aunque dependiente de los hechos), y es una proposición compuesta (condicional).
g) "¡Cierra la puerta inmediatamente!" es una orden, no una afirmación con valor de verdad, por lo que no es una proposición.
h) "O estudias para el examen o reprobarás la materia" es una declaración disyuntiva compuesta por dos proposiciones; tiene un valor de verdad y es una proposición compuesta (disyunción).
i) "Ojalá mañana sea un día soleado" expresa un deseo, no una afirmación que pueda calificarse como verdadera o falsa, por lo tanto no es una proposición.
j) "Lava los platos y seca los cubiertos" es una instrucción compuesta, no una afirmación declarativa, por lo que no es una proposición.
k) "9 < 5" es una desigualdad matemática con un valor de verdad definido (falso), y es una proposición simple.
l) "¡Dame una mano con esto, por favor!" es una solicitud, no una afirmación, por lo que no es una proposición.
m) "El número 2 es par o el número 3 es impar" es una declaración compuesta por dos proposiciones unidas por "o" (disyunción inclusiva); su valor de verdad es verdadero y es una proposición compuesta.
Ejercicio 2
Identificar cuáles de las siguientes son fórmulas válidas en lógica (fórmulas bien formadas).
- (¬p) ∨ q
- p ∧ ∨ q
- p → (¬q ∨ r)
- ¬¬p
- (p ∧ q ∨) r
- ¬(p → (q ∧ ¬r))
- p → → q
- ((p ∨ q) ∧ (¬p ∨ ¬q))
- (p → (q → r)) → ((p → q) → (p → r))
- p ¬ ∧ q
- p ∧ (q ∨ r
- ¬(p ∧ ¬q) ↔ (p → q)
- p ∨ (q ∧ ∨ r)
Soluciones
a) (¬p) ∨ q: es una fórmula bien formada; los paréntesis alrededor de ¬p son redundantes pero no inválidos (¬p ∨ q también sería correcta).
b) p ∧ ∨ q: no es una fórmula bien formada porque el conectivo binario ∧ está seguido inmediatamente por otro conectivo binario ∨, sin un operando entre ellos.
c) p → (¬q ∨ r): es una fórmula bien formada; la estructura sigue las reglas de formación.
d) ¬¬p: es una fórmula bien formada; aplica la negación dos veces sobre p.
e) (p ∧ q ∨) r: no es una fórmula bien formada porque el conectivo ∨ aparece después de q sin un operando a su derecha dentro de la subfórmula, tampoco hay operador conectando a esa subfórmula con r.
f) ¬(p → (q ∧ ¬r)): es una fórmula bien formada; la negación se aplica correctamente a una fórmula compuesta.
g) p → → q: no es una fórmula bien construida porque el conectivo → aparece dos veces consecutivas sin un operando entre ellos.
h) ((p ∨ q) ∧ (¬p ∨ ¬q)): es una fórmula bien formada; los paréntesis son correctos aunque los externos podrían considerarse excesivos.
i) (p → (q → r)) → ((p → q) → (p → r)): es una fórmula bien construida; es una instancia bien construida de un principio lógico.
j) p ¬ ∧ q: no es una fórmula bien formada porque el símbolo de negación ¬ aparece entre p y ∧, violando la sintaxis.
k) p ∧ (q ∨ r: no es una fórmula bien formada porque falta el paréntesis de cierre después de r, dejando la expresión incompleta.
l) ¬(p ∧ ¬q) ↔ (p → q): es una fórmula bien formada; es una equivalencia lógica bien construida.
m) p ∨ (q ∧ ∨ r): no es una fórmula bien formada porque dentro del paréntesis aparece ∧ ∨ r, lo que coloca dos conectivos binarios consecutivos sin operando intermedio.
Formalización de proposiciones
Ejercicio 1
Traducir las siguientes proposiciones dadas en lenguaje cotidiano al lenguaje simbólico de la lógica proposicional.
- La puerta está cerrada pero la ventana está abierta.
- No es cierto que el examen sea mañana.
- Si terminas la tarea, puedes salir a jugar.
- Iremos a la montaña o nos quedaremos en la playa.
- Iré a la fiesta si tú también vas.
- O bien el equipo gana el partido y festejan, o bien pierde y queda eliminado.
- Ni hace frío ni hace calor.
- El cielo está nublado, sin embargo no llueve.
- Para que el motor arranque es necesario que tenga combustible.
- Si el semáforo está en rojo o en amarillo, el coche debe detenerse.
- Si compras la entrada con antelación, ahorrarás dinero; pero si no lo haces, pagarás más.
- Para aprobar el curso es necesario y suficiente que entregues los proyectos y apruebes el examen final.
- Si no te esfuerzas, no progresarás; y si no progresas, no alcanzarás tus metas.
- Si el testigo dice la verdad y el jurado es imparcial, el acusado será liberado; sin embargo, el acusado no será liberado.
- No es cierto que, si el sol brilla, entonces haga frío y la nieve no se derrita.
- Si el presupuesto es aprobado, entonces se construirá el puente si y sólo si los materiales llegan a tiempo.
Soluciones
1) En la proposición "La puerta está cerrada pero la ventana está abierta" identificamos una conjunción; asignamos p: "La puerta está cerrada", q: "la ventana está abierta" y la simbolizamos como p ∧ q, donde "pero" es equivalente a "y".
2) En "No es cierto que el examen sea mañana" identificamos una negación; p: "el examen es mañana" y la simbolizamos como ¬p.
3) En "Si terminas la tarea, puedes salir a jugar" identificamos un condicional; p: "Terminas la tarea", q: "Puedes salir a jugar" y la simbolizamos como p → q, donde p es el antecedente y q el consecuente.
4) En "Iremos a la montaña o nos quedaremos en la playa" identificamos una disyunción inclusiva; p: "Iremos a la montaña", q: "Nos quedaremos en la playa" y la simbolizamos como p ∨ q.
5) En "Iré a la fiesta si tú también vas" identificamos un condicional donde el consecuente aparece primero en la frase; p: "Tú vas a la fiesta", q: "Yo iré a la fiesta" y la simbolizamos como p → q, ya que "iré si tú vas" equivale a "Si tú vas, entonces yo iré".
6) En "O bien el equipo gana el partido y festejan, o bien pierde y queda eliminado" identificamos una disyunción exclusiva (estructura "o bien..., o bien...") entre dos conjunciones; p: "El equipo gana el partido", q: "El equipo festeja", r: "El equipo pierde", s: "El equipo queda eliminado" y la simbolizamos como (p ∧ q) ⊻ (r ∧ s). Nota: "perder" no es lo mismo que "no ganar" (¬p), ya que podría existir empate.
7) En "Ni hace frío ni hace calor" identificamos una negación conjunta, equivalente a "No hace frío y no hace calor"; p: "Hace frío", q: "Hace calor" y la simbolizamos como ¬p ∧ ¬q.
8) En "El cielo está nublado, sin embargo no llueve" identificamos una conjunción con un matiz de contraste; p: "El cielo está nublado", q: "Llueve" y la simbolizamos como p ∧ ¬q, ya que "sin embargo" es equivalente a "y".
9) En "Para que el motor arranque es necesario que tenga combustible" identificamos una condición necesaria; p: "El motor arranca", q: "El motor tiene combustible" y la simbolizamos como p → q, porque "q es necesario para p" equivale a "si p entonces q".
10) En "Si el semáforo está en rojo o en amarillo, el coche debe detenerse" identificamos un condicional con un antecedente compuesto por una disyunción; p: "El semáforo está en rojo", q: "El semáforo está en amarillo", r: "El coche debe detenerse" y la simbolizamos como (p ∨ q) → r.
11) En "Si compras la entrada con antelación, ahorrarás dinero; pero si no lo haces, pagarás más" identificamos una conjunción de dos condicionales; p: "Compras la entrada con antelación", q: "Ahorrarás dinero", r: "Pagarás más" y la simbolizamos como (p → q) ∧ (¬p → r).
12) En "Para aprobar el curso es necesario y suficiente que entregues los proyectos y apruebes el examen final" identificamos un bicondicional donde la condición es una conjunción; p: "Apruebas el curso", q: "Entregas los proyectos", r: "Apruebas el examen final" y la simbolizamos como p ↔ (q ∧ r).
13) En "Si no te esfuerzas, no progresarás; y si no progresas, no alcanzarás tus metas" identificamos una conjunción de dos condicionales encadenados; p: "Te esfuerzas", q: "Progresas", r: "Alcanzas tus metas" y la simbolizamos como (¬p → ¬q) ∧ (¬q → ¬r).
14) En "Si el testigo dice la verdad y el jurado es imparcial, el acusado será liberado; sin embargo, el acusado no será liberado" identificamos una conjunción donde la primera parte es un condicional y la segunda niega su consecuente; p: "El testigo dice la verdad", q: "El jurado es imparcial", r: "El acusado será liberado" y la simbolizamos como ((p ∧ q) → r) ∧ ¬r.
15) En "No es cierto que, si el sol brilla, entonces haga frío y la nieve no se derrita" identificamos la negación de un condicional cuyo consecuente es una conjunción; p: "El sol brilla", q: "Hace frío", r: "La nieve se derrite" y la simbolizamos como ¬(p → (q ∧ ¬r)).
16) En "Si el presupuesto es aprobado, entonces se construirá el puente si y sólo si los materiales llegan a tiempo" identificamos un condicional donde el consecuente es un bicondicional; p: "El presupuesto es aprobado", q: "Se construirá el puente", r: "Los materiales llegan a tiempo" y la simbolizamos como p → (q ↔ r).
Ejercicio 2
Dadas las siguientes proposiciones:
p: "Ana está en el gimnasio"
q: "Bruno está nadando"
r: "Clara juega tenis"
Traducir al lenguaje natural cada una de las siguientes fórmulas:
- p ∧ q
- ¬r
- p → q
- q ∨ r
- ¬p ∧ ¬q
- r ↔ ¬p
- ¬(q ∧ r)
- p → (q ∨ r)
- (p ∧ ¬q) → r
- ¬p ↔ (¬q ∧ ¬r)
Soluciones
- p ∧ q: "Ana está en el gimnasio y Bruno está nadando"
- ¬r: "Clara no juega tenis"
- p → q: "Si Ana está en el gimnasio, entonces Bruno está nadando"
- q ∨ r: "Bruno está nadando o Clara juega tenis"
- ¬p ∧ ¬q: "Ana no está en el gimnasio y Bruno no está nadando"
- r ↔ ¬p: "Clara juega tenis si y sólo si Ana no está en el gimnasio"
- ¬(q ∧ r): "No es cierto que Bruno está nadando y Clara juega tenis"
- p → (q ∨ r): "Si Ana está en el gimnasio, entonces Bruno está nadando o Clara juega tenis"
- (p ∧ ¬q) → r: "Si Ana está en el gimnasio y Bruno no está nadando, entonces Clara juega tenis"
- ¬p ↔ (¬q ∧ ¬r): "Ana no está en el gimnasio si y sólo si Bruno no está nadando y Clara no juega tenis"
Valor de verdad
Ejercicio 1
Sean p = V, q = F y r = V, determinar el valor de verdad de las siguientes proposiciones compuestas:
- p ∧ q
- p ∨ r
- p → q
- ¬r ↔ q
- ¬(q ∨ r)
- (p ∧ ¬q) → r
- q ⊻ p
- (p → q) ∨ (r → q)
- ¬(p ∧ r) → ¬q
- (p ↔ r) ∧ (q → ¬p)
Soluciones
1) p ∧ q: con p = V y q = F, la conjunción es falsa ya que requiere que ambos sean verdaderos, resultado: F.
2) p ∨ r: con p = V y r = V, la disyunción inclusiva es verdadera si al menos uno es verdadero, resultado: V.
3) p → q: con antecedente p = V y consecuente q = F, el condicional es falso, resultado: F.
4) ¬r ↔ q: calculamos ¬r (r = V, entonces ¬r = F) y comparamos con q = F usando bicondicional; es verdadero si ambos valores coinciden (F ↔ F), resultado: V.
5) ¬(q ∨ r): calculamos q ∨ r (F ∨ V = V) y luego negamos: ¬V = F, resultado: F.
6) (p ∧ ¬q) → r: calculamos ¬q (¬F = V), luego p ∧ ¬q (V ∧ V = V); con antecedente V y consecuente r = V, el condicional V → V es verdadero, resultado: V.
7) q ⊻ p: la disyunción exclusiva es verdadera si los valores difieren; con q = F y p = V (F ⊻ V), son diferentes, resultado: V.
8) (p → q) ∨ (r → q): calculamos p → q (V → F = F) y r → q (V → F = F); luego la disyunción F ∨ F es falsa, resultado: F.
9) ¬(p ∧ r) → ¬q: calculamos p ∧ r (V ∧ V = V), luego ¬(p ∧ r) = ¬V = F; calculamos ¬q = ¬F = V; el condicional F → V es verdadero, resultado: V.
10) (p ↔ r) ∧ (q → ¬p): calculamos p ↔ r (V ↔ V = V); calculamos ¬p = ¬V = F, luego q → ¬p (F → F = V); la conjunción V ∧ V es verdadera, resultado: V.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
0,0 / 5 — 0 votos
Ejercicio 2
- Dado que p ∧ q es verdadero, determina el valor de verdad de p → q.
- Suponiendo que p ∨ q es falso, ¿qué valor debe tener ¬p ∧ ¬q?
- Cuando p → q es falso, ¿cuál es el valor resultante de p ↔ q?
- Si p ↔ q es verdadero y p es falso, deduce el valor de q.
- Si p ⊻ q (disyunción exclusiva) es verdadero, ¿qué valor de verdad tiene ¬p ↔ q?
- Si se afirma que ¬(p ∧ q) es verdadero, ¿cuál es el valor de ¬p ∨ ¬q?
- Sabiendo que p → q es verdadero y q es falso, ¿qué se puede concluir sobre p?
- Dado que (p ∧ q) → r es falso, infiere el valor de verdad de r.
Soluciones
1) Dado que p ∧ q es verdadero, implica que p = V y q = V; entonces p → q es V → V, que es verdadero.
2) Si p ∨ q es falso, entonces p = F y q = F; por lo tanto ¬p = V y ¬q = V, así ¬p ∧ ¬q es V ∧ V, que es verdadero.
3) Si p → q es falso, esto solo ocurre cuando p = V y q = F; entonces p ↔ q es V ↔ F, que es falso.
4) Si p ↔ q es verdadero y p es falso (p = F), para que el bicondicional sea verdadero, q debe ser igual a p, es decir, q = F.
5) Si p ⊻ q es verdadero, significa que p y q tienen valores diferentes; si suponemos p = V y q = F, entonces ¬p = F, y ¬p ↔ q es F ↔ F, que es verdadero; si fuera p = F y q = V, ¬p = V, y V ↔ V también es verdadero; en ambos casos la equivalencia es verdadera, por lo tanto ¬p ↔ q es verdadero independientemente de la asignación.
6) Si ¬(p ∧ q) es verdadero, entonces p ∧ q es falso; por las leyes de De Morgan, ¬p ∨ ¬q es equivalente a ¬(p ∧ q), por lo tanto también es verdadero.
7) Si p → q es verdadero y q es falso (q = F), para que el condicional sea verdadero, el antecedente p no puede ser verdadero (porque V→F sería falso), entonces p debe ser falso.
8) Si (p ∧ q) → r es falso, el único caso en que un condicional es falso es cuando el antecedente es verdadero y el consecuente es falso; por lo tanto p ∧ q = V y r = F; entonces r es falso.
Ejercicio 3
- ¿Qué condición deben cumplir p y q para que la fórmula (p → q) ∧ (q → p) sea falsa?
- Determinar los valores de verdad de p y q para que la fórmula [(q ↔ p) ∧ ¬q] → (p ∧ ¬q) sea falsa.
- ¿Bajo qué combinación de valores de p, q y r la proposición (p ∧ q) → (¬r ∧ q) resulta ser falsa?
- ¿Qué relación lógica debe existir entre p y q para que el bicondicional p ↔ (p ∧ q) sea verdadero?
- ¿Existe alguna combinación de valores para p y q que hagan que la fórmula ¬(p ∨ q) ↔ (¬p ∧ ¬q) sea falsa?
Soluciones
1) La fórmula (p → q) ∧ (q → p) es falsa si al menos una de las dos implicaciones es falsa. p → q es falsa solo si p = V y q = F. q → p es falsa solo si q = V y p = F. Por tanto, la conjunción es falsa cuando los valores de p y q son diferentes (p = V, q = F o p = F, q = V).
2) Para que [(q ↔ p) ∧ ¬q] → (p ∧ ¬q) sea falsa, el antecedente debe ser verdadero y el consecuente falso. El antecedente (q ↔ p) ∧ ¬q es verdadero solo si q ↔ p = V y ¬q = V (es decir, q = F). Si q = F, entonces q ↔ p = V implica p = F. Con p = F y q = F, el consecuente p ∧ ¬q es F ∧ V = F. Por lo tanto, la combinación p = F y q = F hace que la fórmula sea falsa.
3) La proposición (p ∧ q) → (¬r ∧ q) es falsa únicamente cuando el antecedente p ∧ q es verdadero y el consecuente ¬r ∧ q es falso. Para que p ∧ q = V, necesitamos p = V y q = V. Con q = V, el consecuente ¬r ∧ q se convierte en ¬r ∧ V, que es falso solo si ¬r es falso, es decir, si r = V. Por lo tanto, la combinación que hace falsa la fórmula es p = V, q = V y r = V.
4) Para que p ↔ (p ∧ q) sea verdadera, p y p ∧ q deben tener el mismo valor de verdad. Si p es falso, p ∧ q también es falso, lo que hace verdadero el bicondicional. Si p es verdadero, entonces p ∧ q es verdadero solo si q es verdadero. Por tanto, la relación es que la fórmula es verdadera cuando p es falso, o cuando tanto p como q son verdaderos. Equivalentemente, es verdadera siempre que no ocurra que p sea verdadero y q falso.
5) La fórmula ¬(p ∨ q) ↔ (¬p ∧ ¬q) es una tautología (una de las leyes de De Morgan), lo que significa que es verdadera para cualquier combinación de valores de p y q. Por lo tanto, no existe ninguna combinación que la haga falsa.
Tablas de verdad
Construir las tablas de verdad de las siguientes proposiciones y determinar si son tautologías, contingencias o contradicciones.
- (p ∧ q) → p
- (¬p ∧ q) ↔ (q ∨ ¬q)
- ¬(p ∧ q → p)
- (¬p ∧ q) → r
- (p → q) ∧ (q → r) → (p → r)
Solución 1
| p | q | p ∧ q | (p ∧ q) → p |
|---|---|---|---|
| V | V | V | V |
| V | F | F | V |
| F | V | F | V |
| F | F | F | V |
Se trata de una tautología.
Solución 2
| p | q | ¬p | ¬q | ¬p ∧ q | q ∨ ¬q | (¬p ∧ q) ↔ (q ∨ ¬q) |
|---|---|---|---|---|---|---|
| V | V | F | F | F | V | F |
| V | F | F | V | F | V | F |
| F | V | V | F | V | V | V |
| F | F | V | V | F | V | F |
Corresponde a una contingencia.
Solución 3
| p | q | p ∧ q | p ∧ q → p | ¬(p ∧ q → p) |
|---|---|---|---|---|
| V | V | V | V | F |
| V | F | F | V | F |
| F | V | F | V | F |
| F | F | F | V | F |
Se trata de una contradicción.
Solución 4
| p | q | r | ¬p | ¬p ∧ q | (¬p ∧ q ) → r |
|---|---|---|---|---|---|
| V | V | V | F | F | V |
| V | V | F | F | F | V |
| V | F | V | F | V | V |
| V | F | F | F | F | V |
| F | V | V | V | V | V |
| F | V | F | V | V | F |
| F | F | V | V | F | V |
| F | F | F | V | F | V |
Corresponde a una contingencia.
Solución 5
| p | q | r | p → q | q → r | p → r | (p → q) ∧ (q → r) | [(p → q) ∧ (q → r)] → (p → r) |
|---|---|---|---|---|---|---|---|
| V | V | V | V | V | V | V | V |
| V | V | F | V | F | F | F | V |
| V | F | V | F | V | V | F | V |
| V | F | F | F | V | F | F | V |
| F | V | V | V | V | V | V | V |
| F | V | F | V | F | V | F | V |
| F | F | V | V | V | V | V | V |
| F | F | F | V | V | V | V | V |
Se trata de una tautología.
Recomendados:
Equivalencias lógicas
Demostrar las siguientes equivalencias lógicas:
- ¬¬p ≡ p
- p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
- ¬(p ∧ q) ≡ ¬p ∨ ¬q
- ¬(p ∨ q) ≡ ¬p ∧ ¬q
- p → q ≡ ¬p ∨ q
- p ↔ q ≡ (p → q) ∧ (q → p)
Si queremos demostrar que A ≡ B, podemos construir una tabla de verdad para verificar que A ↔ B sea siempre verdadera (tautología).
Solución 1
| p | ¬p | ¬¬p | ¬¬p ↔ p |
|---|---|---|---|
| V | F | V | V |
| F | V | F | V |
Solución 2
| p | q | r | q ∨ r | p ∧ (q ∨ r) | p ∧ q | p ∧ r | (p ∧ q) ∨ (p ∧ r) | [p ∧ (q ∨ r)] ↔ [(p ∧ q) ∨ (p ∧ r)] |
|---|---|---|---|---|---|---|---|---|
| V | V | V | V | V | V | V | V | V |
| V | V | F | V | V | V | F | V | V |
| V | F | V | V | V | F | V | V | V |
| V | F | F | F | F | F | F | F | V |
| F | V | V | V | F | F | F | F | V |
| F | V | F | V | F | F | F | F | V |
| F | F | V | V | F | F | F | F | V |
| F | F | F | F | F | F | F | F | V |
Solución 3
| p | q | p ∧ q | ¬(p ∧ q) | ¬p | ¬q | ¬p ∨ ¬q | [¬(p ∧ q)] ↔ [¬p ∨ ¬q] |
|---|---|---|---|---|---|---|---|
| V | V | V | F | F | F | F | V |
| V | F | F | V | F | V | V | V |
| F | V | F | V | V | F | V | V |
| F | F | F | V | V | V | V | V |
Solución 4
| p | q | p ∨ q | ¬(p ∨ q) | ¬p | ¬q | ¬p ∧ ¬q | [¬(p ∨ q)] ↔ [¬p ∧ ¬q] |
|---|---|---|---|---|---|---|---|
| V | V | V | F | F | F | F | V |
| V | F | V | F | F | V | F | V |
| F | V | V | F | V | F | F | V |
| F | F | F | V | V | V | V | V |
Solución 5
| p | q | p → q | ¬p | ¬p ∨ q | (p → q) ↔ (¬p ∨ q) |
|---|---|---|---|---|---|
| V | V | V | F | V | V |
| V | F | F | F | F | V |
| F | V | V | V | V | V |
| F | F | V | V | V | V |
Solución 6
| p | q | p ↔ q | p → q | q → p | (p → q) ∧ (q → p) | [p ↔ q] ↔ [ (p → q) ∧ (q → p)] |
|---|---|---|---|---|---|---|
| V | V | V | V | V | V | V |
| V | F | F | F | V | F | V |
| F | V | F | V | F | F | V |
| F | F | V | V | V | V | V |
Simplificación de proposiciones
Reducir las siguientes fórmulas proposicionales a su mínima expresión aplicando leyes del álgebra proposicional.
- (p ∧ p) ∨ q
- ¬(¬p ∧ q) ∧ p
- (p ∨ q) ∧ (p ∨ ¬q)
- p → (p ∧ q)
- (p ∧ q) ∨ (p ∧ ¬q)
- ¬(p → ¬q)
- [p ∧ (q ∨ p)] ∨ q
- ¬(¬p ∨ ¬q)
- (p ∨ q) ∧ ¬(¬p ∧ ¬q)
- (p ∨ V) ∧ (q ∨ F) (Nota: V es una tautología y F una contradicción)
Solución 1
(p ∧ p) ∨ q
≡ p ∨ q (Ley de idempotencia: p ∧ p ≡ p)
Solución 2
¬(¬p ∧ q) ∧ p
≡ (¬¬p ∨ ¬q) ∧ p (Ley de De Morgan)
≡ (p ∨ ¬q) ∧ p (Doble negación: ¬¬p ≡ p)
≡ p ∧ (p ∨ ¬q) (Conmutatividad de ∧)
≡ p (Ley de absorción: p ∧ (p ∨ ¬q) ≡ p)
Solución 3
(p ∨ q) ∧ (p ∨ ¬q)
≡ p ∨ (q ∧ ¬q) (Ley distributiva de ∨ sobre ∧)
≡ p ∨ F (Ley de complemento: q ∧ ¬q ≡ F)
≡ p (Ley de identidad: p ∨ F ≡ p)
Solución 4
p → (p ∧ q)
≡ ¬p ∨ (p ∧ q) (Implicación: p → r ≡ ¬p ∨ r)
≡ (¬p ∨ p) ∧ (¬p ∨ q) (Ley distributiva de ∨ sobre ∧)
≡ V ∧ (¬p ∨ q) (Ley de complemento: ¬p ∨ p ≡ V)
≡ ¬p ∨ q (Ley de identidad: V ∧ r ≡ r)
≡ p → q (Implicación)
Solución 5
(p ∧ q) ∨ (p ∧ ¬q)
≡ p ∧ (q ∨ ¬q) (Ley distributiva de ∧ sobre ∨)
≡ p ∧ V (Ley de complemento: q ∨ ¬q ≡ V)
≡ p (Ley de identidad: p ∧ V ≡ p)
Solución 6
¬(p → ¬q)
≡ ¬(¬p ∨ ¬q) (Implicación: p→¬q ≡ ¬p ∨ ¬q)
≡ ¬¬p ∧ ¬¬q (Ley de De Morgan)
≡ p ∧ q (Doble negación)
Solución 7
[p ∧ (q ∨ p)] ∨ q
≡ [p ∧ (p ∨ q)] ∨ q (Conmutatividad de ∨)
≡ p ∨ q (Ley de absorción: p ∧ (p ∨ q) ≡ p, luego p ∨ q)
Solución 8
¬(¬p ∨ ¬q)
≡ ¬¬p ∧ ¬¬q (Ley de De Morgan)
≡ p ∧ q (Doble negación)
Solución 9
(p ∨ q) ∧ ¬(¬p ∧ ¬q)
≡ (p ∨ q) ∧ (¬¬p ∨ ¬¬q) (Ley de De Morgan)
≡ (p ∨ q) ∧ (p ∨ q) (Doble negación)
≡ p ∨ q (Ley de idempotencia)
Solución 10
(p ∨ V) ∧ (q ∨ F)
≡ V ∧ q (Ley de dominación: p ∨ V ≡ V; Ley de identidad: q ∨ F ≡ q)
≡ q (Ley de identidad: V ∧ q ≡ q)
Inferencia y validez de argumentos
Ejercicio 1
Traducir al lenguaje simbólico los siguientes argumentos y determinar si son válidos o inválidos.
- Si cocino, podré comer. Cociné. Por lo tanto, podré comer.
- Si estudio mucho, apruebo el examen. No estudio mucho. Luego, no apruebo el examen.
- Si el equipo juega bien, gana el partido. Si gana el partido, hay fiesta. Así que, si el equipo juega bien, hay fiesta.
- O vamos al cine o al restaurante. No vamos al cine. Por consiguiente, vamos al restaurante.
- Si el semáforo está en rojo, los coches se detienen. Los coches se detienen. Entonces, el semáforo está en rojo.
- Si hay sol, llevo gafas de sol. No llevo gafas de sol. Por tanto, no hay sol.
- Si aprieto este botón, se enciende la luz. Si se enciende la luz, puedo leer. No puedo leer. Luego, no he apretado el botón.
- Si el alimento está envenenado, el perro no lo come. El perro no come el alimento. Por consiguiente, el alimento está envenenado.
- Si es fin de semana, duermo hasta tarde. Si duermo hasta tarde, desayuno a mediodía. No desayuno a mediodía. Así que, no es fin de semana.
- Si hoy es martes, mañana es miércoles. Mañana no es miércoles. Por lo tanto, hoy no es martes.
- Si voy al médico, entonces me recetará medicina. Si me receta medicina, mejoraré. No mejoraré o debo pagar la factura. Voy al médico. Por lo tanto, debo pagar la factura.
- O estudio lógica o estudio matemáticas. Si estudio lógica, entonces comprendo los argumentos. Si estudio matemáticas, entonces resuelvo problemas. No comprendo los argumentos. Por tanto, resuelvo problemas.
- Si hace frío, entonces llevo abrigo. Si llevo abrigo, entonces no tengo frío o estoy de moda. Tengo frío. Hace frío. Por lo tanto, estoy de moda.
- Si ahorro dinero, viajaré en verano. Si viajo en verano, aprenderé un idioma. O no aprendo un idioma o conoceré gente nueva. Ahorro dinero. Por consiguiente, conoceré gente nueva.
Solución 1
Sea p: "Cocino", q: "Puedo comer".
El argumento es: Si cocino, podré comer (p → q). Cociné (p). Por lo tanto, podré comer (q).
Formalmente: [(p → q) ∧ p] → q.
Esto corresponde al modus ponens, una regla de inferencia válida. Por tanto, el argumento es válido.
Solución 2
Sea p: "Estudio mucho", q: "Apruebo el examen".
El argumento es: Si estudio mucho, apruebo el examen (p → q). No estudio mucho (¬p). Luego, no apruebo el examen (¬q).
Formalmente: [(p → q) ∧ ¬p] → ¬q.
Esto es la falacia de negar el antecedente, que no es una regla válida. Un contraejemplo: si q es verdadero aunque p sea falso, las premisas serían verdaderas pero la conclusión falsa. Por tanto, el argumento es inválido.
Solución 3
Sea p: "El equipo juega bien", q: "El equipo gana el partido", r: "Hay fiesta".
El argumento es: Si el equipo juega bien, entonces gana el partido (p → q). Si gana el partido, entonces hay fiesta (q → r). Así que, si el equipo juega bien, entonces hay fiesta (p → r).
Formalmente: [(p → q) ∧ (q → r)] → (p → r).
Esto corresponde a la ley del silogismo hipotético, una regla de inferencia válida. Por tanto, el argumento es válido.
Solución 4
Sea p: "Vamos al cine", q: "Vamos al restaurante".
El argumento es: O vamos al cine o al restaurante (p ∨ q). No vamos al cine (¬p). Por consiguiente, vamos al restaurante (q).
Formalmente: [(p ∨ q) ∧ ¬p] → q.
Esto corresponde a la regla de silogismo disyuntivo, que es válida. Por tanto, el argumento es válido.
Solución 5
Sea p: "El semáforo está en rojo", q: "Los coches se detienen".
El argumento es: Si el semáforo está en rojo, los coches se detienen (p → q). Los coches se detienen (q). Por lo tanto, el semáforo está en rojo (p).
Formalmente: [(p → q) ∧ q] → p.
Esto es la falacia de afirmar el consecuente, que no es válida. Un contraejemplo: los coches pueden detenerse por otra razón (por ejemplo, un peatón) aunque el semáforo no esté en rojo. Por tanto, el argumento es inválido.
Solución 6
Sea p: "Hay sol", q: "Llevo gafas de sol".
El argumento es: [(p → q) ∧ ¬q] → ¬p.
Esto corresponde al modus tollens, una regla de inferencia válida. Por tanto, el argumento es válido.
Solución 7
Sea p: "Aprieto este botón", q: "Se enciende la luz", r: "Puedo leer".
El argumento es: [(p → q) ∧ (q → r) ∧ ¬r] → ¬p.
Aplicamos modus tollens a (q → r) y ¬r para obtener ¬q. Luego, aplicamos modus tollens a (p → q) y ¬q para obtener ¬p. Esta cadena de inferencias es válida. Por tanto, el argumento es válido.
Solución 8
Sea p: "El alimento está envenenado", q: "El perro no come el alimento".
El argumento es: [(p → q) ∧ q] → p.
Esto es la falacia de afirmar el consecuente, que no es válida. El perro puede no comer por otras razones. Por tanto, el argumento es inválido.
Solución 9
Sea p: "Es fin de semana", q: "Duermo hasta tarde", r: "Desayuno a mediodía".
El argumento es: [(p → q) ∧ (q → r) ∧ ¬r] → ¬p.
Aplicamos modus tollens a (q → r) y ¬r para obtener ¬q. Luego, aplicamos modus tollens a (p → q) y ¬q para obtener ¬p. Esta inferencia es válida. Por tanto, el argumento es válido.
Solución 10
Sea p: "Hoy es martes", q: "Mañana es miércoles".
El argumento es: [(p → q) ∧ ¬q] → ¬p.
Esto es modus tollens, una regla válida. Por tanto, el argumento es válido.
Solución 11
Sea p: "Voy al médico", q: "Me recetará medicina", r: "Mejoraré", s: "Debo pagar la factura".
El argumento es: [(p → q) ∧ (q → r) ∧ (¬r ∨ s) ∧ p] → s.
De p y p → q se infiere q (modus ponens). De q y q → r se infiere r (modus ponens). De r y ¬r ∨ s se infiere s (por silogismo disyuntivo, ya que r hace falso el primer disyunto (¬r), obligando a que s sea verdadero). Por tanto, el argumento es válido.
Solución 12
Sea p: "Estudio lógica", q: "Estudio matemáticas", r: "Comprendo los argumentos", s: "Resuelvo problemas".
El argumento es: [(p ∨ q) ∧ (p → r) ∧ (q → s) ∧ ¬r] → s.
De ¬r y p→r, por modus tollens, se infiere ¬p. De ¬p y p ∨ q, por silogismo disyuntivo, se infiere q. De q y q→s, por modus ponens, se infiere s. Por tanto, el argumento es válido.
Solución 13
Sea p: "Hace frío", q: "Llevo abrigo", r: "Tengo frío", s: "Estoy de moda".
El argumento es: [(p → q) ∧ (q → (¬r ∨ s)) ∧ r ∧ p] → s.
De p y p→q se infiere q. De q y q→(¬r ∨ s) se infiere ¬r ∨ s. De r se tiene que ¬r es falso, por lo tanto, para que ¬r ∨ s sea verdadero, s debe ser verdadero. Esto es una aplicación válida del silogismo disyuntivo. Por tanto, el argumento es válido.
Solución 14
Sea p: "Ahorro dinero", q: "Viajaré en verano", r: "Aprenderé un idioma", s: "Conoceré gente nueva".
El argumento es: [(p → q) ∧ (q → r) ∧ (¬r ∨ s) ∧ p] → s.
Este argumento tiene la misma estructura lógica que el ejercicio 11, por lo que es válido.
Ejercicio 2
Deducir la conclusión de los siguientes razonamientos.
- Si Juan estudia todos los días, entonces aprobará el examen. Si aprueba el examen, sus padres le regalarán una bicicleta. Juan estudia todos los días. ¿Qué recibirá Juan de sus padres?
- El testamento está en el despacho o está en la caja de seguridad. Si estuviera en el despacho, la secretaria lo habría visto. La secretaria afirma no haber visto ningún documento. ¿Dónde está el testamento?
- Si el sospechoso huyó por la ventana, hay marcas en el jardín. Si hay marcas en el jardín, el perro habría ladrado. El perro permaneció en absoluto silencio toda la noche. ¿Huyó el sospechoso por la ventana?
- El problema del coche es la batería o es el alternador. Si fuera la batería, las luces estarían tenues. Las luces brillan con total intensidad. ¿Cuál es el problema del coche?
- Si la clínica está abierta, el Dr. García está en su consultorio. Si el Dr. García está en su consultorio, su coche está en el estacionamiento. El estacionamiento está completamente vacío. ¿Está abierta la clínica?
- O cocinamos pasta o pedimos pizza. Si cocinamos pasta, tardaremos una hora. Tenemos mucha hambre y no podemos esperar una hora. ¿Qué terminaremos comiendo?
- Si el planeta tiene agua líquida, podría albergar vida. Si podría albergar vida, es un objetivo prioritario para la NASA. Los telescopios confirman que el planeta tiene agua líquida. ¿Es el planeta un objetivo prioritario?
- Si un triángulo es equilátero, entonces tiene tres ángulos de 60°. El triángulo ABC tiene un ángulo de 90°. ¿Es el triángulo ABC equilátero?
Solución 1
Por modus ponens, si Juan estudia todos los días (confirmado), entonces aprobará el examen. Luego, aplicando modus ponens nuevamente, si aprueba el examen, sus padres le regalarán una bicicleta. Por lo tanto, se concluye que Juan recibirá una bicicleta de sus padres. También se podría haber aplicado silogismo hipotético.
Solución 2
El testamento está en el despacho o en la caja de seguridad. Si estuviera en el despacho, la secretaria lo habría visto; pero la secretaria afirma no haberlo visto, por lo tanto, por modus tollens, no está en el despacho. Entonces, por silogismo disyuntivo, el testamento está en la caja de seguridad.
Solución 3
Si el sospechoso huyó por la ventana, entonces habría marcas en el jardín. Si hubiera marcas, el perro habría ladrado. El perro permaneció en silencio, por lo tanto, por modus tollens aplicado a la segunda implicación, no hay marcas en el jardín. Luego, aplicando modus tollens a la primera implicación, el sospechoso no huyó por la ventana.
Solución 4
El problema es la batería o el alternador. Si fuera la batería, las luces estarían tenues. Las luces brillan con intensidad, por lo tanto, por modus tollens, no es la batería. Por silogismo disyuntivo, el problema del coche es el alternador.
Solución 5
Si la clínica está abierta, el Dr. García está en su consultorio. Si está en su consultorio, su coche está en el estacionamiento. El estacionamiento está vacío, por lo tanto, por modus tollens aplicado a la segunda implicación, el Dr. García no está en su consultorio. Luego, aplicando modus tollens a la primera implicación, la clínica no está abierta.
Solución 6
O cocinamos pasta o pedimos pizza. Si cocinamos pasta, tardaremos una hora. No podemos esperar una hora, por lo tanto, por modus tollens, no cocinamos pasta. Por silogismo disyuntivo, terminaremos pidiendo pizza.
Solución 7
Si el planeta tiene agua líquida, podría albergar vida. Si pudiera albergar vida, es un objetivo prioritario. Los telescopios confirman que tiene agua líquida, por lo tanto, por modus ponens aplicado a la primera implicación, podría albergar vida. Luego, por modus ponens aplicado a la segunda implicación, se concluye que el planeta es un objetivo prioritario para la NASA.
Solución 8
Si un triángulo es equilátero, entonces tiene tres ángulos de 60°. El triángulo ABC tiene un ángulo de 90°, lo que implica que no tiene tres ángulos de 60°. Por modus tollens, se concluye que el triángulo ABC no es equilátero.
Bibliografía
- Acevedo González, G. (2011). Lógica matemática. Universidad Nacional Abierta y a Distancia (UNAD).
- Castillo P., E. y Pinta, M. (2015). Lógica matemática I: proposiciones y leyes de inferencia (2.ª ed.). Universidad Técnica de Machala.
- Copi, I. y Cohen, C. (2013). Introducción a la lógica (2.ª ed.). Limusa.
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones elementales de lógica matemática y teoría de conjuntos. Fondo Editorial OPSU.
- Daun, J. y Falcón, Y. (1995). Lógica matemática. Universidad Autónoma Metropolitana.
- Garrido, M. (1974). Lógica simbólica (4.ª ed.). Tecnos.
- Gentile, E. (1984). Notas de álgebra I. Editorial Universitaria de Buenos Aires.
- Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
- Puyau, H. y Roetti, J. (1976). Elementos de lógica matemática. Editorial Universitaria de Buenos Aires.
- Rojo, A. (1996). Álgebra I (18.ª ed.). El Ateneo.
¿Te ha servido este contenido? ¡Califícalo!
0,0 / 5 — 0 votos
CÓMO CITAR ESTE ARTÍCULO
Machado, D. (2026, 7 de febrero). Ejercicios resueltos de lógica proposicional. Flamath. https://es.flamath.com/ejercicios-logica-proposicional
Deja una respuesta

Otros artículos que te pueden interesar