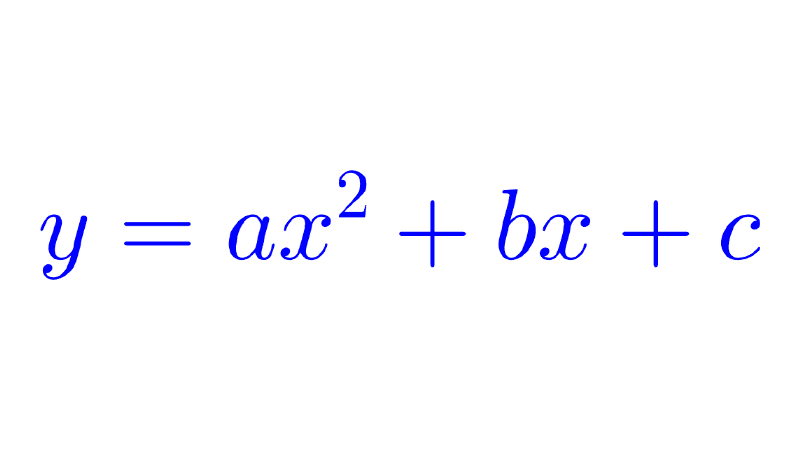
Vértice de una función cuadrática
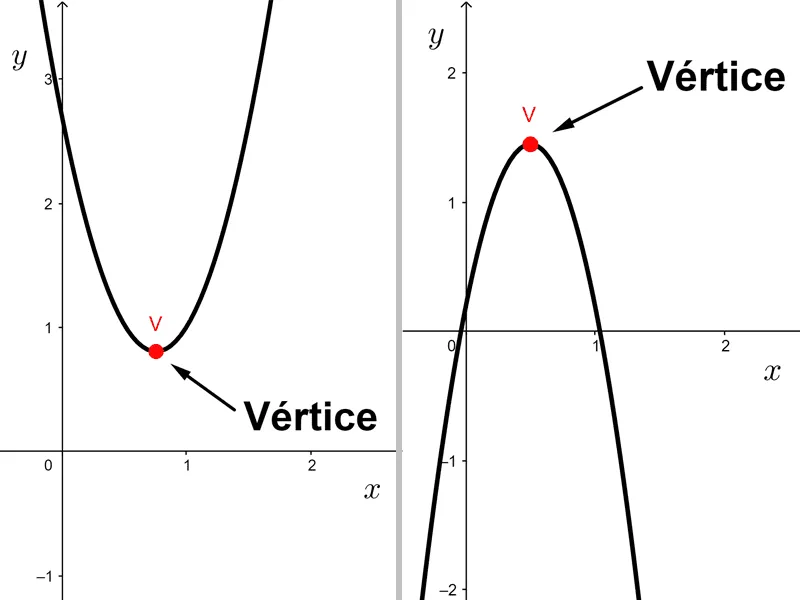
El vértice de una función cuadrática es un punto extremo de su gráfica, que es una parábola. Este punto representa el valor mínimo o máximo de la función, dependiendo de la orientación de la parábola.
Dada una función f(x) = ax2 + bx + c, el vértice es el punto más bajo del gráfico (valor mínimo) si la parábola se abre hacia arriba (a > 0); y es el punto más alto del gráfico (valor máximo) si la parábola se abre hacia abajo (a < 0).
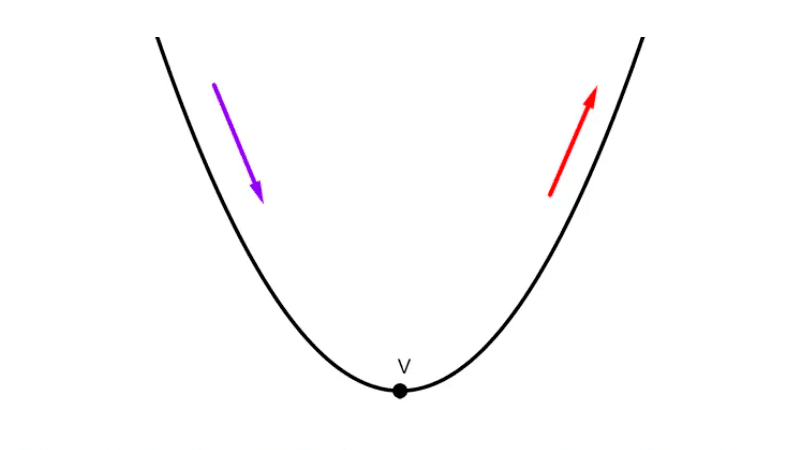
El vértice también es también el punto de inflexión donde la función pasa de ser creciente a ser decreciente (o viceversa) y este punto se encuentra sobre el eje de simetría, la recta que divide la parábola en dos partes simétricas.
Dada una función cuadrática f(x) = ax2 + bx + c, las coordenadas (h, k) del vértice se pueden obtener con las siguientes fórmulas:
h = -b / (2a)
k = f(h)
Es decir que podemos seguir los siguientes pasos para calcular el vértice:
- Identificar los coeficientes a, b y c de la función cuadrática f(x) = ax2 + bx + c.
- Calcular la coordenada x del vértice (h) utilizando la fórmula: h = -b / (2a).
- Calcular la coordenada y del vértice (k) sustituyendo el valor de h en la función original: k = f(h). El vértice es el punto V(h, k).
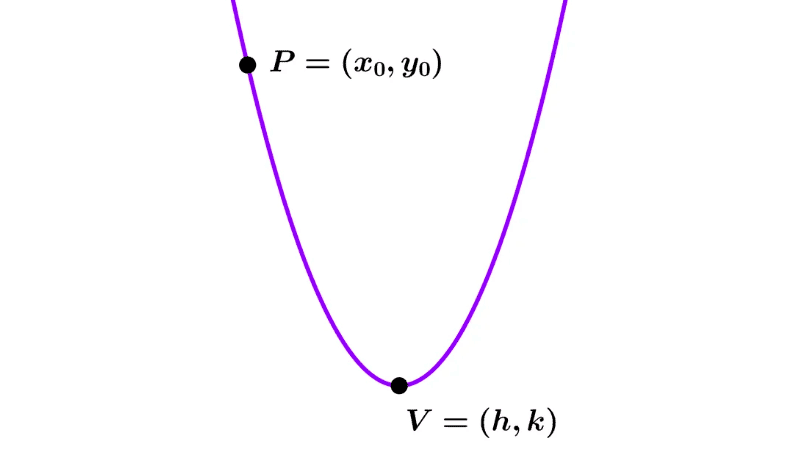
Si la función está dada en forma canónica f(x) = a(x - h)² + k (también llamada estándar o forma vértice), las coordenadas del vértice V(h, k) pueden extraerse de forma directa de allí.
Ejercicios resueltos
Ejercicio 1
Hallar el vértice de la función *f(x)=-2x^2+8x-5* y determinar si este es máximo o mínimo.
Solución
Identificamos los coeficientes que necesitamos: *a=-2,b=8* y los reemplazamos en la fórmula del vértice:
*h=\dfrac{-b}{2a}=\dfrac{-8}{2\cdot(-2)}=\dfrac{-8}{-4}=2*
*k=f(h)=f(2)=-2(2)^2+8(2)-5=3*
Por tanto, el vértice de *f* es *V=(2,3).* Por ser *a* un número negativo, el vértice corresponde al máximo de la función.
Ejercicio 2
Determine el vértice de la función *f(x)=\dfrac{3}{4}x^2-2x+9*
Solución
Identificamos los coeficientes que usaremos: *a=\dfrac{3}{4}, b=-2* y los sustituimos en la fórmula:
*h=\dfrac{-b}{2a}=\dfrac{-(-2)}{2\cdot\dfrac{3}{4}}=\dfrac{2}{\dfrac{3}{2}}=\dfrac{4}{3}*
*k=f(h)=f\left(\dfrac{4}{3}\right)=\dfrac{3}{4}\cdot\left(\dfrac{4}{3}\right)^2-2\cdot\left(\dfrac{4}{3}\right)+9=\dfrac{23}{3}*
El vértice es entonces *V=\left(\dfrac{4}{3},\dfrac{23}{3}\right).* Por ser *a* un número positivo, el vértice corresponde a un mínimo de la función.
Ejercicio 3
Calcular el vértice de la función *f(x)=x^2+3* y determinar si es mínimo o máximo.
Solución
En este caso tenemos una función cuadrática incompleta, pues uno de los coeficientes vale cero. Extraemos los que utilizaremos: *a=1, b=0* y sacamos las coordenadas del vértice:
*h=\dfrac{-b}{2a}=\dfrac{-0}{2\cdot1}=0*
*k=f(h)=f(0)=(0)^2+3=3*
El vértice de es *V=(0,3)* y, por ser *a* positivo, corresponde al mínimo de *f.*
Ejercicio 4
Sacar el vértice de la función *f(x)=-6x^2*
Solución
Otra vez tenemos una función cuadrática incompleta, pues dos coeficientes valen cero. Identificamos los que usaremos: *a=-6, b=0* y sustituimos en la fórmula:
*h=\dfrac{-b}{2a}=\dfrac{-0}{2(-6)}=0*
*k=f(h)=-6(0)^2=0*
Entonces, el vértice es *V=(0,0)* y corresponde a un máximo por ser *a* un número negativo.
Bibliografía
- Chorny, F., Casares, P. y Salpeter, C. (2015). Matemática 4. Editorial Estrada.
- Effenberger, P. (2016). Matemática III. Kapelusz Editora.
- Entre Números III. (2016). Santillana.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta


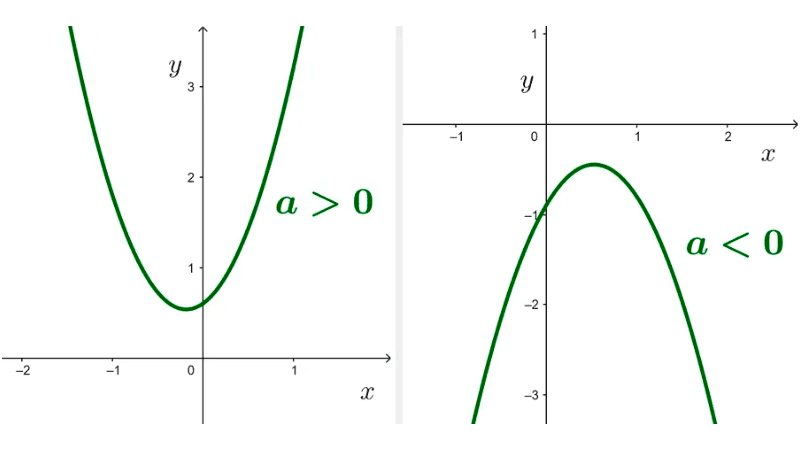
Otros artículos que te pueden interesar