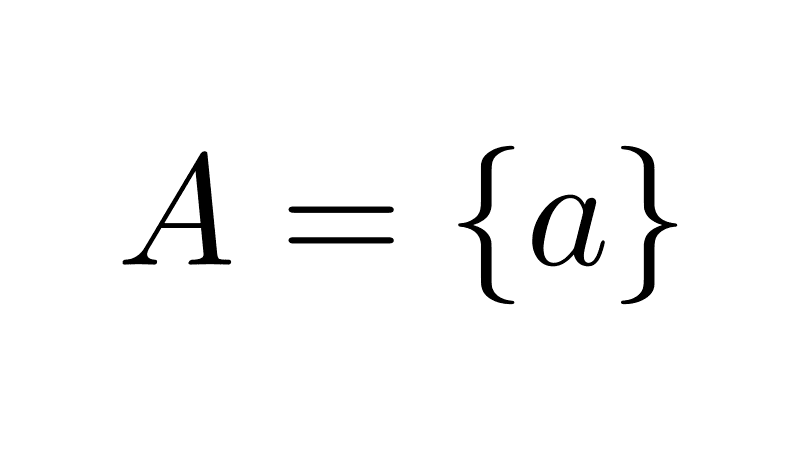
Subconjunto de un conjunto
Un subconjunto es una colección de elementos que están totalmente contenidos dentro de otro conjunto, que puede ser más grande o no. Por ejemplo, el conjunto {1, 2} es subconjunto de {1, 2, 3}, porque todos los elementos del primero están también en el segundo.
Existen dos tipos de subconjuntos: propios e impropios. Un subconjunto propio es aquel cuyos elementos están dentro de otro conjunto, pero este último tiene elementos que no están en el primero, es decir que no pueden ser conjuntos iguales. Un subconjunto impropio es aquel que es idéntico al conjunto original.
Índice
Definición formal
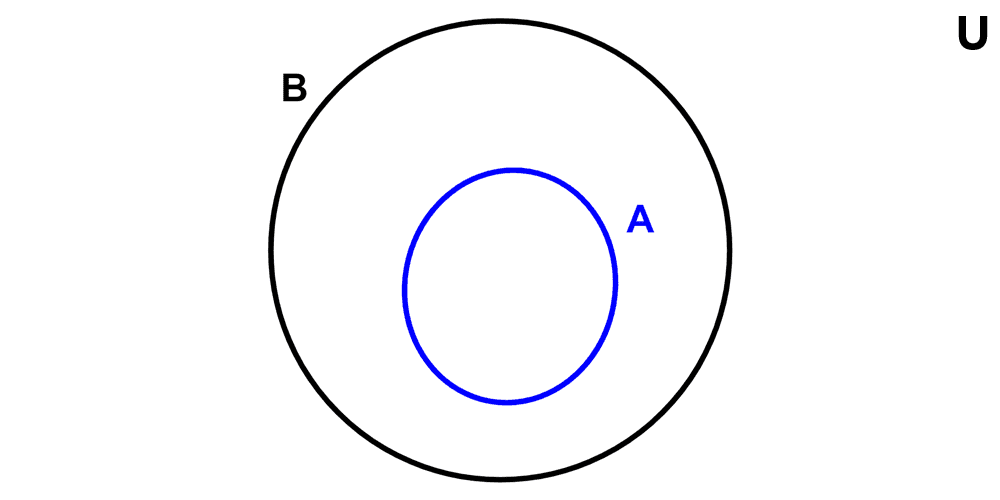
Un conjunto A es subconjunto de B otro si todo elemento del A es también un elemento de B, esta relación se simboliza con ⊆ (inclusión amplia):
A ⊆ B si y sólo si ∀x: (x ∈ A → x ∈ B)
También podemos decir que un conjunto B es un superconjunto de un conjunto A (se escribe B ⊇ A) si y solo si todo elemento de A también es un elemento de B. En otras palabras: B es superconjunto de A exactamente cuando A es subconjunto de B.
Si existe al menos un elemento de A que no está en B, entonces se dice que A no es un subconjunto de B y se simboliza como A ⊈ B.
Ejemplos
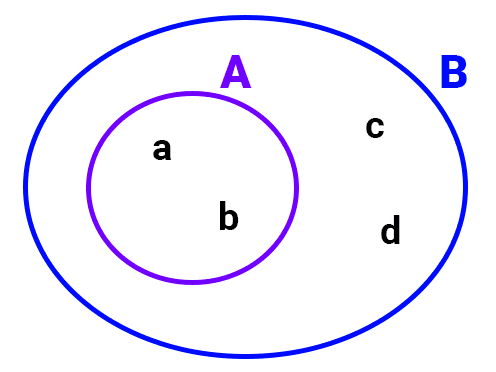
- El conjunto A = {a, b} es subconjunto de B = {a, b, c, d} porque los elementos de A están también dentro de B, entonces A ⊆ B.
- El conjunto de todos los mamíferos tiene por subconjunto al conjunto de todos los seres humanos, porque todo ser humano es un mamífero.
- El conjunto C = {0, 1, 2, 3} es un subconjunto de D = {-1, 0, 1, 2, 3, a, b}, porque todo elemento de C también está contenido en D, entonces C ⊆ D.
- El conjunto de todas las plantas es un subconjunto del conjunto de todos los seres vivos.
- El conjunto P = {p, q, r, s} no es un subconjunto de Q = {p, r} porque P tiene elementos que no están en Q, entonces: P ⊈ Q. Sin embargo, podemos notar que Q sí es un subconjunto de P, entonces Q ⊆ P.
- El conjunto M = {-1, 1} es un subconjunto de N = {1, -1}: M ⊆ N; y, a su vez N es un subconjunto de M: N ⊆ M. Cuando esto ocurre se dice que ambos conjuntos son iguales: M = N. En otros términos, M es subconjunto impropio de N.
- El conjunto de los números naturales es un subconjunto del conjunto de los números enteros, pues todo número natural es también un número entero, entonces N ⊆ Z. Sin embargo, como existen enteros que no son naturales (los negativos y el cero), la relación recíproca no es cierta, Z no es subconjunto de N: Z ⊈ N.
- El conjunto de todos los reales positivos R+ es un subconjunto de números reales, porque todo número real positivo es también un número real: R+ ⊆ R.
- Si llamamos T al conjunto de todos los triángulos, se tiene que el conjunto E de los triángulos equiláteros es un subconjunto de T: E ⊆ T.
- El conjunto vacío se considera un subconjunto impropio de sí mismo: ∅ ⊆ ∅. También, el vacío es subconjunto de cualquier conjunto: ∅ ⊆ A para todo conjunto A.
Para demostrar que un conjunto es subconjunto de otro, es necesario probar que todo elemento del primero es también un elemento del segundo. Para demostrar que un conjunto no es subconjunto de otro, basta con encontrar un elemento del primero que no esté en el segundo.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
El conjunto que contiene a todos los subconjuntos de A se llama conjunto potencia o conjunto de partes de A, y se simboliza como P(A). Si A tiene n elementos, su conjunto potencia tiene 2n elementos. Es decir, el número de subconjuntos de un conjunto de n elementos es 2n. Por ejemplo, si A = {1, 2, 3}, su conjunto potencia P(A) = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}. En este caso, el número de subconjuntos es 23 = 8.
Subconjunto propio
Un conjunto es subconjunto propio de otro si todos los elementos del primero son también elementos del segundo, pero existen elementos del segundo que no están en el primero, es decir que no pueden ser conjuntos iguales. Esta relación se simboliza con ⊂ (inclusión estricta) o ⊊:
A ⊂ B si y solo si ∀x: (x ∈ A → x ∈ B) y además A ≠ B
Si existe al menos un elemento de A que no está en B, o ocurre que A y B son iguales, entonces se dice que A no es un subconjunto propio de B y se simboliza como A ⊄ B.
Ejemplos
- El conjunto A = {a, b} es subconjunto propio de B = {a, b, c, d} porque los elementos de A están también dentro de B y hay elementos de B que no están en A ("c" y "d"). Entonces A ⊂ B. Nótese que también ocurre que A ⊆ B.
- El conjunto M = {-1, 1} es no es un subconjunto propio de N = {1, -1} porque ambos conjuntos son iguales, entonces M ⊄ N. Sin embargo, ocurre que M ⊆ N, es decir, M es subconjunto de N, pero no es un subconjunto propio.
- El conjunto de todos los seres humanos que hablan español es un subconjunto propio del conjunto de todos los seres humanos.
- El conjunto de los números naturales, además de ser un subconjunto de los números enteros, también es un subconjunto propio de él: N ⊂ Z.
- El conjunto P de los números pares es un subconjunto propio de los números enteros (P ⊂ Z), ya que existen enteros que no son pares.
- El conjunto de los números racionales (Q) es un subconjunto propio de los números reales (R): Q ⊂ R, porque existen números irracionales (como π o √2) en R que no están en Q.
- El intervalo [0, 1] es un subconjunto propio del intervalo [-1, 2]: [0, 1] ⊂ [-1, 2], porque [-1, 2] contiene números menores que 0 y mayores que 1 que no están en [0, 1].
- El intervalo (5, 10) es un subconjunto propio del intervalo [5, 10), es decir: (5,10) ⊂ [5,10), porque el segundo conjunto incluye el número 5, que no está en el primero.
- El conjunto de todos los cuadrados es un subconjunto propio del conjunto de todos los rectángulos (Cuadrados ⊂ Rectángulos), porque un cuadrado es un caso especial de rectángulo, pero existen rectángulos que no son cuadrados (aquellos con lados de diferente longitud).
- El conjunto de todas las circunferencias es un subconjunto propio del conjunto de todas las elipses, ya que existen elipses que no son circunferencias.
Todo subconjunto propio es también un subconjunto, como en el primer ejemplo, pero no todo subconjunto es un subconjunto propio, como en el segundo ejemplo.
Propiedades de los subconjuntos
Los subconjuntos cumplen con las propiedades de la inclusión de conjuntos:
- Reflexividad: todo conjunto es subconjunto de sí mismo, es decir, A ⊆ A.
- Antisimetría: si un conjunto es subconjunto de otro y este también es subconjunto del primero, entonces ambos conjuntos son iguales. Es decir, si A ⊆ B y B ⊆ A, entonces A = B.
- Transitividad: si un conjunto es subconjunto de otro, y éste a su vez es subconjunto de un tercero, entonces el primer conjunto también es subconjunto del tercero. Es decir, si A ⊆ B y B ⊆ C, entonces A ⊆ C.
- El conjunto vacío es subconjunto de cualquier conjunto, hasta de sí mismo. O sea, Ø ⊆ A y Ø ⊆ Ø.
- Todos los conjuntos son subconjuntos del universal U: A ⊆ U.
Simbología
A continuación, se resume la simbología utilizada para referirnos a subconjuntos.
| Símbolo | Significado |
|---|---|
| A ⊆ B | A es subconjunto de B |
| A ⊈ B | A no es subconjunto de B |
| B ⊇ A | B es superconjunto de A |
| A ⊂ B | A es un subconjunto propio de B |
| A ⊄ B | A no es un subconjunto propio de B |
Nota: la simbología A ⊆ B y A ⊂ B no se utiliza uniformemente en matemáticas. A veces el símbolo ⊆ se usa para indicar subconjuntos y otras veces para indicar subconjuntos propios, lo mismo ocurre con el símbolo ⊂. También es importante reconocer que los símbolos de contención (⊆ y ⊂) se usan para relacionar dos conjuntos entre sí, no para relacionar un elemento con un conjunto, para eso se usa ∈ (que se lee "pertenece").
Bibliografía
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
- Daun, J. y Falcón, Y. (1995). Lógica matemática. Universidad Autónoma Metropolitana.
- Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
- Grimaldi, R. (1997). Matemáticas discreta y combinatoria (3ra edición). Addison-Wesley Iberoamericana.
- Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
- Puyau, H. y Roetti, J. (1976). Elementos de Lógica Matemática. Editorial Universitaria de Buenos Aires.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.
- Vidal, J. (2010). Teoría de conjuntos. Universidad de Valencia.
- Wilches, L., Costa, R., Rincón, M., Acosta, M., Roa, J., Sulvara, J. y Jaime, D. (2013). Matemática 6. Editorial Santillana.
- Zill, D. y Dewar, J. (2012). Álgebra, trigonometría y geometría analítica (3ra edición). McGraw Hill.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

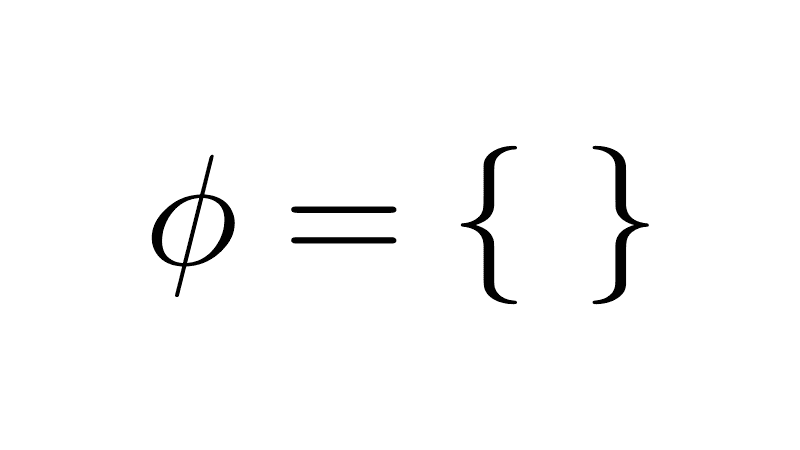
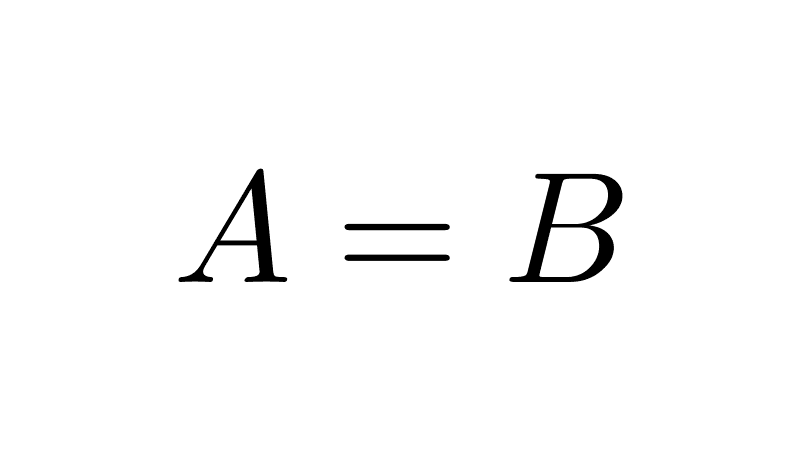
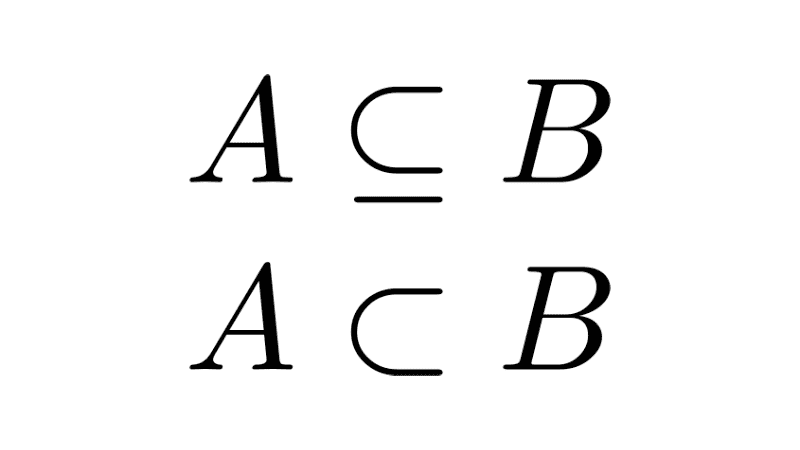
Otros artículos que te pueden interesar