Diferencia simétrica de conjuntos

La diferencia simétrica de conjuntos es una operación que produce un nuevo conjunto formado por los elementos que se encuentran en uno de los conjuntos originales, pero no en ambos. Se representa con el símbolo Δ, que corresponde a la letra griega delta mayúscula y tiene forma de triángulo.

Alternativamente, la diferencia simétrica puede entenderse como la unión de los conjuntos menos su intersección:

A Δ B = (A ∪ B) - (A ∩ B)

Otra forma equivalente de definirla es combinando las diferencias simples entre los conjuntos:

A Δ B = (A - B) ∪ (B - A)

Ejemplos

Para calcular la diferencia simétrica, podemos emplear dos métodos equivalentes, que siempre conducen al mismo resultado:

Método 1: calcular la unión de los conjuntos y restar su intersección, siguiendo esta fórmula:

A Δ B = (A ∪ B) - (A ∩ B)

Método 2: unir las dos diferencias simples entre los conjuntos, siguiendo esta otra fórmula:

A Δ B = (A - B) ∪ (B - A)

A continuación, veremos varios casos aplicando estos procedimientos.

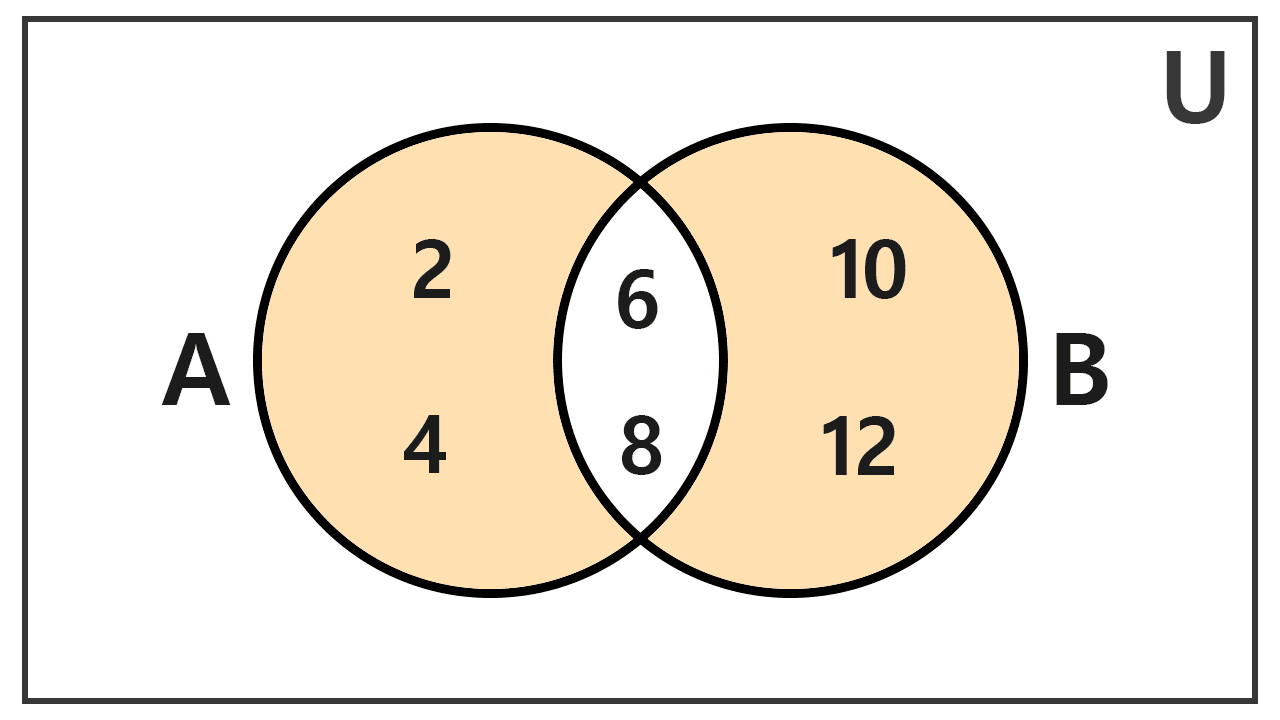
Ejemplo 1

Sean los conjuntos A = {2, 4, 6, 8} y B = {6, 8, 10, 12}. Hallar su diferencia simétrica.

Solución

Aplicaremos ambos métodos para comprobar que el resultado es el mismo.

Método 1: (A ∪ B) - (A ∩ B)

Primero, encontramos la unión de A y B: A ∪ B = {2, 4, 6, 8, 10, 12}.

Luego, identificamos su intersección: A ∩ B = {6, 8}.

Finalmente, restamos la intersección a la unión: 

(A ∪ B) - (A ∩ B) = {2, 4, 6, 8, 10, 12} - {6, 8} = {2, 4, 10, 12}

Método 2: (A - B) ∪ (B - A)

Calculamos los elementos que están solo en A: A - B = {2, 4}.

Calculamos los elementos que están solo en B: B - A = {10, 12}.

Unimos ambos resultados: 

(A - B) ∪ (B - A) = {2, 4} ∪ {10, 12} = {2, 4, 10, 12}

Ambos métodos confirman que la diferencia simétrica es:

A Δ B = {2, 4, 10, 12}

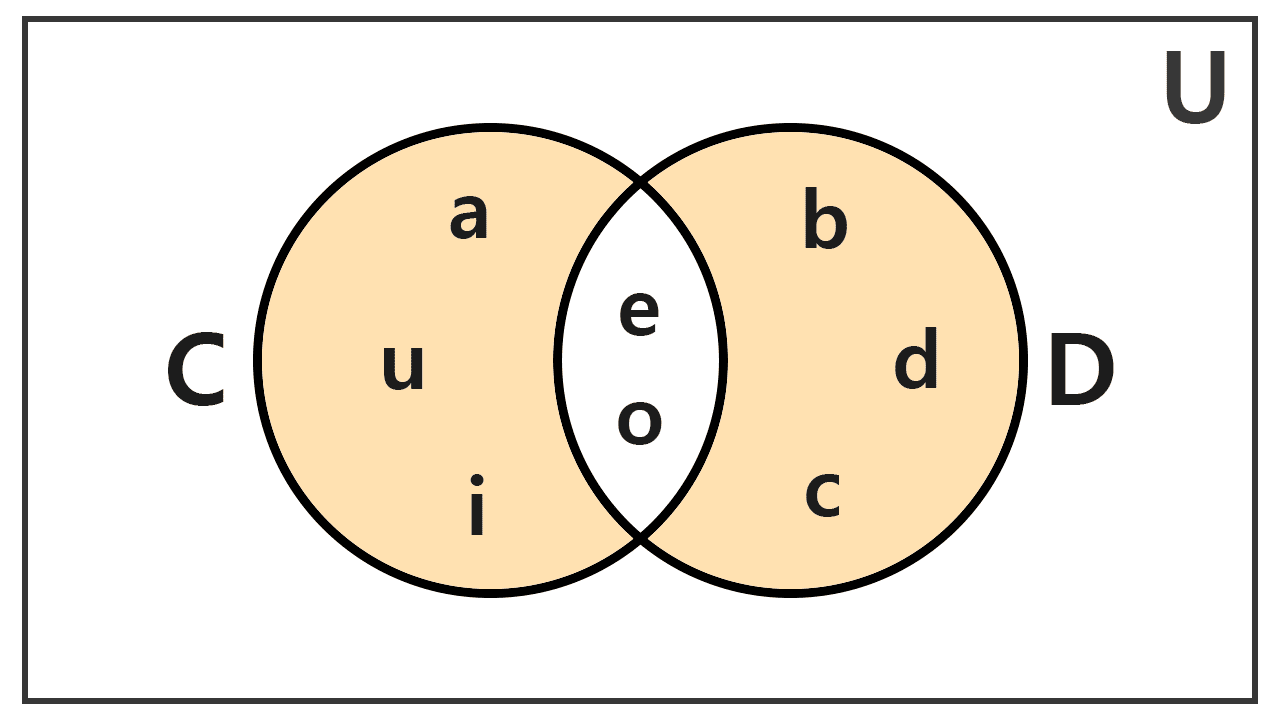
Ejemplo 2

Determinar la diferencia simétrica de C = {a, e, i, o, u} y D = {e, o, b, c, d}.

Solución

Usaremos el método de unir las diferencias simples. Para ello, primero buscamos los elementos exclusivos de C: 

C - D = {a, i, u}

Ahora identificamos los elementos exclusivos de D: 

D - C = {b, c, d}

La unión de estos dos conjuntos da el resultado:

C Δ D = {a, i, u, b, c, d}

Ejemplo 3

Calcular la diferencia simétrica de E = {1, 3, 5} y F = {2, 4, 6}.

Solución

Aplicamos el método de la unión menos la intersección.

La unión es E ∪ F = {1, 2, 3, 4, 5, 6}.

Dado que no tienen elementos en común, su intersección es vacía: E ∩ F = ∅.

Restar el conjunto vacío no altera el conjunto, por lo tanto:

E Δ F = {1, 2, 3, 4, 5, 6} - ∅ = {1, 2, 3, 4, 5, 6}

Ejemplo 4

Sean los conjuntos P = {10, 20, 30, 40} y Q = {5, 10, 15, 20}. Obtener P Δ Q.

Solución

Calculamos la unión y la intersección.

P ∪ Q = {5, 10, 15, 20, 30, 40}

P ∩ Q = {10, 20}

La diferencia simétrica es la unión sin la intersección:

P Δ Q = {5, 10, 15, 20, 30, 40} - {10, 20} = {5, 15, 30, 40}

Ejemplo 5

Determinar la diferencia simétrica de A = {x ∈ N | x es par ∧ x < 10} y B = {x ∈ N | x es múltiplo de 3 ∧ x < 10}.

Solución

Primero expresamos ambos conjuntos por extensión:

A = {2, 4, 6, 8}

B = {3, 6, 9}

Ahora, usamos el método de unir las diferencias simples.

A - B = {2, 4, 8}

B - A = {3, 9}

Uniendo ambos resultados, obtenemos:

A Δ B = {2, 3, 4, 8, 9}

Ejemplo 6

Hallar la diferencia simétrica de P = {x ∈ Z | -2 ≤ x ≤ 2} y Q = {x ∈ N | x² < 10}.

Solución

Comenzamos por listar los elementos de cada conjunto.

P incluye los números enteros desde -2 hasta 2: P = {-2, -1, 0, 1, 2}.

Q contiene los números naturales cuyo cuadrado es menor que 10: Q = {1, 2, 3}.

Aplicamos el método de la unión menos la intersección.

P ∪ Q = {-2, -1, 0, 1, 2, 3}

P ∩ Q = {1, 2}

Por lo tanto, la diferencia simétrica es:

P Δ Q = (P ∪ Q) - (P ∩ Q) = {-2, -1, 0, 1, 2, 3} - {1, 2} = {-2, -1, 0, 3}

Propiedades

La operación de diferencia simétrica en la teoría de conjuntos posee características notables que facilitan su manipulación y cálculo.

1) Conmutatividad: el orden de los conjuntos no altera el resultado.

A Δ B = B Δ A

2) Asociatividad: la forma de agrupar los conjuntos no afecta al conjunto final.

(A Δ B) Δ C = A Δ (B Δ C)

3) Elemento neutro: la diferencia simétrica de cualquier conjunto con el conjunto vacío es el conjunto original.

A Δ ∅ = A

4) Elemento inverso: todo conjunto es su propio inverso para esta operación, la diferencia simétrica de un conjunto consigo mismo da como resultado el conjunto vacío.

A Δ A = ∅

5) Intersección distributiva: la intersección es distributiva respecto a la diferencia simétrica.

A ∩ (B Δ C) = (A ∩ B) Δ (A ∩ C)

6) Relación con conjuntos disjuntos: si dos conjuntos son disjuntos (no tienen elementos en común), su diferencia simétrica es igual a su unión.

Si A ∩ B = ∅, entonces A Δ B = A ∪ B

7) Relación con subconjuntos: si un conjunto es subconjunto de otro, la diferencia simétrica se reduce a la diferencia de conjuntos simple.

Si A ⊆ B, entonces A Δ B = B - A

Si B ⊆ A, entonces A Δ B = A - B

8) Ley de cancelación: si la diferencia simétrica de dos conjuntos con un tercero es igual, entonces los dos conjuntos originales son iguales.

Si A Δ C = B Δ C, entonces A = B