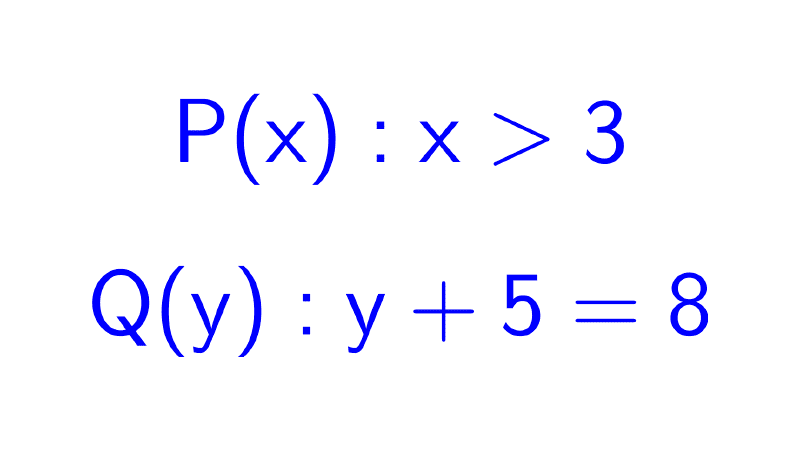
Cuantificadores lógicos

Los cuantificadores lógicos son símbolos utilizados en lógica matemática que permiten especificar la cantidad de elementos de un conjunto que satisfacen una determinada propiedad o predicado. Transforman funciones proposicionales (enunciados abiertos con variables) en proposiciones completas con valor de verdad definido.

Una función proposicional, como P(x): "x es primo", no es una proposición ya que su valor de verdad depende del valor de x. Los cuantificadores permiten convertirla en una proposición al especificar cuántos elementos del dominio cumplen la propiedad.

Tipos de cuantificadores

Los dos cuantificadores más utilizados son el universal y el existencial. También existe un caso especial de este último conocido como cuantificador de existencia única.

Cuantificador universal (∀)

El cuantificador universal se utiliza para afirmar que una propiedad se cumple para todos los elementos de un conjunto o dominio, sin excepción. Su símbolo es ∀ (una "A" invertida, proviene de la palabra alemana Allgemein, que significa "para todos" o "general"). Su lectura habitual es "para todo", "para cada", "todo", "siempre".

La forma general es ∀x: P(x) donde P(x) es una función proposicional, se interpreta como: "para todo x, P(x) es verdadero" o "para todo x, se verifica P(x)".

El universo de discurso (o dominio) es el conjunto de elementos sobre los que se cuantifica. Definirlo es esencial, ya que el significado de una proposición depende completamente de este. Si tenemos un universo de discurso U, podemos incluirlo directamente en el enunciado cuantificado: ∀x ∈ U: P(x).

Una proposición cuantificada universalmente es verdadera si todos los elementos del universo de discurso cumplen la condición indicada. Si existe al menos un elemento que no la cumpla, el enunciado es falso.

Este cuantificador permite crear frases del estilo "todos los humanos son mortales", "todas las plantas son seres vivos", "todos los argentinos son latinoamericanos", etc. Veremos a continuación ejemplos aplicados en matemáticas.

Ejemplos

1. ∀x ∈ N: x > 0 dice que "para todo número natural x, se verifica que x es mayor a cero", esto es verdadero.
2. ∀x ∈ R: x ≥ 1 afirma que todo número real es mayor o igual a 1; esto es falso, porque existen números reales menores a 1.
3. ∀x ∈ R: x² ≥ 0 dice que el cuadrado de todo número real es mayor o igual a cero. Esta es una proposición verdadera, ya que el cuadrado de cualquier número real es siempre un número no negativo.
4. "∀x ∈ Z: 2x es par" afirma que, para todo número entero, se cumple que su doble es par. Esta es una proposición verdadera, pues cualquier entero multiplicado por 2 resulta en un número par por definición.
5. ∀x ∈ R: sen²(x) + cos²(x) = 1 significa que para todo número real se cumple la identidad trigonométrica fundamental, esta es una proposición verdadera.
6. ∀n ∈ N: n + 1 > n nos dice que al sumar 1 a cualquier número natural, el resultado es siempre mayor que el número original. Esto es verdadero.

Cuantificador existencial (∃)

El cuantificador existencial se utiliza para expresar que existe al menos un elemento en el universo del discurso que cumple cierta propiedad o predicado. Su símbolo es ∃, que proviene de la letra "E" invertida de la palabra inglesa exists ("existe"). La lectura habitual es "existe", "hay al menos un" o "existe al menos un elemento tal que...".

La forma general de este cuantificador se escribe como: ∃x | P(x) y significa que hay algún valor de x dentro del universo considerado que hace verdadera la proposición P(x).

Una proposición que contiene el cuantificador ∃ es verdadera si se puede encontrar al menos un elemento en el universo del discurso que cumpla la condición indicada. No importa si la cumplen varios elementos o incluso todos; basta con que exista uno.

Este cuantificador permite crear frases del tipo "existen personas jóvenes", "existen muebles de madera", "existen gatos anaranjados", etc. A continuación, veremos ejemplos aplicados en matemáticas.

Ejemplos

1. ∃x ∈ R | x² = 4 significa "existe un número real cuyo cuadrado es 4", esto es verdadero: 2 es un ejemplo, -2 también.
2. "∃n ∈ N / n es par y primo" nos dice que existe al menos un número natural par y primo, de nuevo, esto es verdadero: 2 es un caso (de hecho, el único).
3. ∃x ∈ Z | x + 5 = 0 expresa que existe un número entero que sumado con 5 da 0, esto es cierto, pues -5 es ese número.
4. ∃y ∈ Q / y² = 2 dice que existe un número racional cuyo cuadrado es 2. Esta proposición es falsa, ya que √2 es irracional.
5. ∃x ∈ R | x³ = 27 afirma que existe un número real cuyo cubo es 27, en este caso x = 3, así que la proposición es verdadera.
6. ∃x ∈ R / x² = -1 expresa que existe un número real que elevado al cuadrado resulta en -1. Esta proposición es falsa, porque todo número real elevado al cuadrado es no negativo. Si el universo de discurso fuera el conjunto de los números complejos (C), sería una proposición verdadera.

Cuantificador de unicidad (∃!)

El cuantificador de unicidad, también llamado cuantificador de existencia única, se utiliza para afirmar que existe exactamente un elemento en el universo del discurso que cumple cierta condición. Su símbolo habitual es ∃!, que se lee como "existe un único", "existe exactamente uno" o "hay un solo".

La forma general es: ∃! x | P(x) y significa que dentro del universo de discurso hay un solo valor de x que hace verdadera la proposición P(x).

Una proposición con ∃! será verdadera únicamente si se cumplen dos cosas:

• Existe al menos un elemento que satisface la propiedad.
• Ese elemento es único, es decir, no hay dos ni más que la cumplan.

Ejemplos

1. ∃! n ∈ N | n es par y primo significa "existe un único número natural que es par y primo". Esto es verdadero, porque solo el número 2 cumple esa condición.
2. ∃! x ∈ R | x² = 4 afirma que "existe un único número real cuyo cuadrado es 4". Esto es falso, ya que tanto 2 como -2 cumplen la condición, así que no es único.
3. ∃! n ∈ N | n > 1000 significa "existe un único número natural mayor que 1000". Esto es falso, porque hay infinitos números naturales mayores que 1000.
4. ∃! n ∈ N | n = 7 dice "existe un único número natural que es igual a 7". Esto es verdadero, porque solo el número 7 cumple la proposición.
5. ∃! x ∈ Z | x + 5 = 0 dice "existe un único número entero que sumado con 5 da 0". Esto es verdadero, porque solo x = -5 cumple la condición.
6. ∃! y ∈ Q | y² = 2 afirma que "existe un único número racional cuyo cuadrado es 2". Esto es falso, porque en realidad no existe ningún número racional con esa propiedad.

Los cuantificadores alcanzan a la función proposicional que tengan más cerca, salvo que lo modifiquen signos de agrupación (paréntesis, corchetes, llaves). Por ejemplo: ∀x: P(x) ∨ Q(x) se interpreta como [∀x: P(x)] ∨ Q(x). Si quisiéramos que el cuantificador alcance a las dos funciones, debemos escribir ∀x: [ P(x) ∨ Q(x) ].

Negación de cuantificadores

Negar una afirmación cuantificada significa invertir el cuantificador y, al mismo tiempo, negar el predicado. Este principio se aplica al cuantificador universal (∀) y al cuantificador existencial (∃). En cuanto al cuantificador de unicidad (∃!), se lo considera un caso particular del existencial, por lo que su negación se resuelve de manera derivada, no directa.

Negación del cuantificador universal

¬[∀x: P(x)] ≡ ∃x | ¬P(x)

Es decir: "no es cierto que todos los x cumplen P(x)" equivale a "existe al menos un x que no cumple P(x)".

Intuitivamente, decir que "no es cierto que todos los cisnes son blancos" es lógicamente equivalente a decir "existe al menos un cisne que no es blanco". Basta con un solo contraejemplo para refutar una afirmación universal.

Ejemplos

1) ¬(∀x ∈ R | x² > 0) ≡ ∃x ∈ R | ¬(x² > 0)

Aquí, "no es cierto que para todo número real su cuadrado sea mayor que 0" equivale a decir "existe al menos un número real cuyo cuadrado no es mayor que 0". Esto es verdadero, ya que x = 0 es un contraejemplo (0² = 0 no es mayor que 0). Sabiendo esto podríamos escribir: ∃x ∈ R | x² = 0.

2) ¬(∀n ∈ N | n es primo) ≡ ∃n ∈ N | ¬(n es primo) ≡ ∃n ∈ N | n no es primo

En este caso, "no es cierto que todos los números naturales sean primos" equivale a "existe al menos un número natural que no es primo". Esto es verdadero, por ejemplo n = 4 no es primo.

3) ¬(∀x ∈ Z | x² es impar) ≡ ∃x ∈ Z | x² es par

En este ejemplo, "no es cierto que todos los enteros elevados al cuadrado sean impares" equivale a afirmar que "existe al menos un entero cuyo cuadrado no es impar". Esto es verdadero, ya que x = 2 lo cumple (2² = 4, que es par).

Negación del cuantificador existencial

¬[∃x | P(x)] ≡ ∀x: ¬P(x)

Es decir: "no es cierto que existe algún x que cumple P(x)" equivale a "todos los x no cumplen P(x)".

En el lenguaje cotidiano, decir "no es cierto que existan dragones que escupan fuego" es lo mismo que afirmar "todos los dragones no escupen fuego", o más simple aún, "ningún dragón escupe fuego".

Ejemplos

1) ¬(∃n ∈ N | n < 0) ≡ ∀n ∈ N | ¬(n < 0)

En este caso vemos que "no es cierto que exista un número natural menor que 0" equivale a "todos los números naturales no son menores que 0". Esto es verdadero, porque los naturales empiezan en 1 (o en 0 según la convención) y ninguno es negativo.

2) ¬(∃x ∈ Q | x² = 2) ≡ ∀x ∈ Q | x² ≠ 2

Aquí, "no es cierto que exista un número racional cuyo cuadrado sea 2" equivale a "para todo número racional, su cuadrado no es 2". Esto es verdadero, porque √2 no es racional.

3) ¬(∃x ∈ R | x² = -1) ≡ ∀x ∈ R | x² ≠ -1

En este caso, "no es cierto que exista un número real cuyo cuadrado sea -1" equivale a decir "para todo número real, su cuadrado no es -1". Esto es verdadero, porque ningún real satisface x² = -1.

Los casos de negación se resumen en la siguiente tabla.

Caso	Cómo se hace	Simbología
Negación del cuantificador universal	Se cambia por existencial y se niega el predicado	¬[∀x: P(x)] ≡ ∃x | ¬P(x)
Negación del cuantificador existencial	Se cambia por universal y se niega el predicado	¬[∃x | P(x)] ≡ ∀x: ¬P(x)

Combinación de cuantificadores

En una proposición lógica pueden aparecer varios cuantificadores al mismo tiempo, incluso combinando existenciales (∃) y universales (∀). Cuando los cuantificadores son del mismo tipo (todos ∀ o todos ∃), el orden no altera el significado. En cambio, cuando los cuantificadores son mixtos (∃ y ∀), el orden sí importa, y puede cambiar el sentido de la proposición.

Para ilustrarlo, consideremos un predicado genérico P(x, y). Los cuatro esquemas principales son:

1) ∀x ∀y: P(x, y) que se lee "para toda x y para toda y se cumple P(x, y)".

Por ejemplo, la propiedad conmutativa de la suma y la multiplicación de números reales se expresa así:

∀x ∈ R ∀y ∈ R: x + y = y + x

∀x ∈ R ∀y ∈ R: x · y = y · x

2) ∃x ∃y | P(x, y) se lee "existen una x y una y que cumplen P(x, y)".

Un ejemplo es: ∃x ∈ Z ∃y ∈ Z | x² + y² = 25. Esto es verdadero, porque x = 3, y = 4 cumplen la ecuación.

3) ∀x ∃y | P(x, y) se lee "para toda x existe una y que cumple P(x, y)".

Por ejemplo: ∀x ∈ R ∃y ∈ R | x + y = 0. Esto es verdadero, porque para cualquier número real x siempre existe un y = -x que lo anula en la suma (el opuesto).

4) ∃x ∀y: P(x, y) se lee "existe una x tal que para toda y se cumple P(x, y)"

Ejemplo: ∃x ∈ R ∀y ∈ R: x · y = 0. Esto es verdadero, porque si x = 0, sin importar qué valor tome y, el producto es siempre 0.

Bibliografía

• Acevedo González, G. (2011). Lógica Matemática. Universidad Nacional Abierta y a Distancia (UNAD).
• Castillo P, E. y Pinta, M. (2015). Lógica Matemática I: Proposiciones y Leyes de Inferencia (2da edición). Universidad Técnica de Machala.
• Copi, I. y Cohen, C. (2013). Introducción a la Lógica (2da edición). Limusa.
• Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
• Daun, J. y Falcón, Y. (1995). Lógica matemática. Universidad Autónoma Metropolitana.
• Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
• Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.